show brief video of chemical reactions (colors or explosion or lots of smoke would be cool)
Then a question similar to this one…
Show a simple experiment…discuss either or all (controls, variable, correlation,…)
ACT Math Tip: Proficiency with fractions is a good way to pick up quick points on the #ACT. #36U #math
On screen: A lizard slowly walks 1/4 of the way to the grass then spots a cat. It scurries the remaining distance in 5 equal segments. How long were those segments?
ACT English Tip
Avoiding Extraneous Punctuation
(8.16.2019)
Lengthy sentences don’t always require lots of punctuation. Use punctuation only to make communication clearer. #distractorchoices #English #36U #ACTPrep
ACT Math Tip
Vectors: Direction and Magnitude
(5.9.2019)
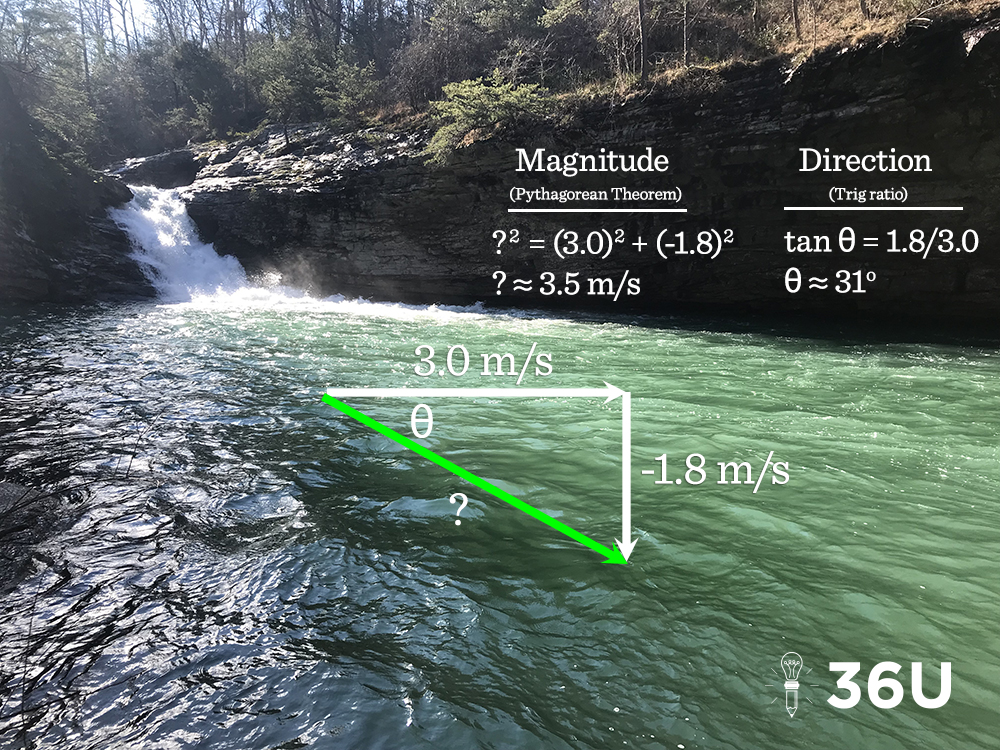
Brush up on your right triangle skills to handle the most difficult of vector items! #newACTcontent #math #ACT #36U
Step 1: Use the Pythagorean theorem to find the magnitude of the vector.
The vector’s magnitude is approximately 3.5 meters per second.
Step 2: Use a trig ratio to find the direction of the vector.
In this case, we set up the tangent ratio to find the missing angle. The vector’s direction is approximately 31 degrees south of east.
English Tip – Redundancy
3.25.19
One of the easiest ways to eliminate answer choices on ACT English test? Eliminate redundancy! #English #ACT #36U
The phrase “caused by all of the precipitation” restates information given earlier in the sentence. On the ACT, find the answer choice that does not contain the redundancy.
ACT Math Tip – Period and Amplitude
(2.11.2019)
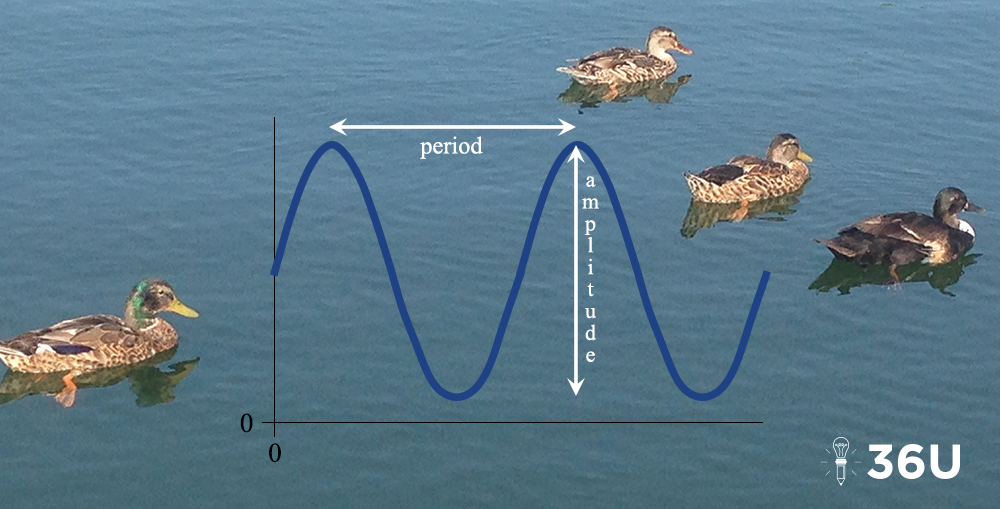
Recognize period and amplitude from trig graphs—even if you haven’t had Advanced Algebra! #mathmonday #math #ACT #ACTPrep #36U
period = distance for function to complete one full cycle
amplitude = difference between maximum and minimum function values
36U Challenge Items
November 2018
ACT Math: Expected Value Challenge
ACT Math: Expected Value Challenge Item – Solution
January 2017
ACT Math: The 100 Lockers Problem
ACT Math: The Solution to the 100 Lockers Problem
Expected Value Challenge Item Winter Challenge
November 2018
Solution Page
We at 36U want to thank the many students and teachers who participated in our November 2018 Winter Challenge. We hope you enjoyed working the item and learned a new skill or two along the way!
For those who missed it, here was the challenge problem:
The Problem
In a fountain, there are 1,000 quarters, 2,000 dimes, 2,000 nickels, and 5,000 pennies. A student randomly draws a coin from the fountain each day for 3 years, records its value, and tosses it back into the fountain.
Let x equal the value of a coin drawn randomly from the fountain. If all coins are equally likely to be drawn, regardless of coin size, what is the expected value (long-run average) of x?
A. 1¢
B. 4¢
C. 6¢
D. 8¢
E. 10¢
The Solution
The expected value, or long-run average, of coins drawn randomly from the fountain is 6 cents.
Almost every submission was correct. Great work!
Here’s how we worked the item:
Step 1: Find the probability of each outcome.
The first step in solving expected value items is to find the probability of each outcome. Often, the ACT will provide those probabilities in a probability distribution table.
Finding the probabilities will allow us to weight each outcome in Step 2.
Here’s the probability of each outcome:
P(penny) = 5,000 pennies/10,000 total coins = 1/2
P(nickel) = 2,000 nickels/10,000 total coins = 1/5
P(dime) = 2,000 dimes/10,000 total coins = 1/5
P(quarter) = 1,000 quarters/10,000 total coins = 1/10
Step 2: Weight each outcome.
Now that you know the probability of each outcome, weight each outcome value by multiplying by its probability.
One-half of the time, the student draws a penny that is worth 1 cent.
1/2 • 1¢ –> .5¢
One-fifth of the time, the student draws a nickel that is worth 5 cents.
1/5 • 5¢ –> 1¢
One-fifth of the time, the student draws a dime that is worth 10 cents.
1/5 • 10¢ –> 2¢
One-tenth of the time, the student draws a quarter that is worth 25 cents.
1/10 • 25¢ –> 2.5¢
Step 3: Add the values.
The probabilities add to 1. When we multiplied the probabilites by the values, we essentially broke down a single draw from the fountain into all the possible outcomes, weighted, of course.
Now it’s time to add those values to see what an average draw from the fountain would give.
Expected value = .5¢ + 1¢ + 1¢ + 2.5¢
Expected value = 6¢
The expected value, or long-run average, of a coin drawn randomly from the fountain is 6¢.
Impressive solution!
One of our favorite problem solving approaches came via Facebook. Check it out.
The Winner
Congratulations to Bailey S., our November 2018 Expected ValueChallenge winner! Her solution was simple, precise, and just as important, correct. Here’s what she had to say:
The Winnings!
Bailey won the 36U Winter Care Package:
1 month of access to 36U ACT Prep
36U Tee (Long-sleeve)
$15 Starbucks gift card
Expected Value Challenge Item Giveaway
November 2018
Statistics and probability are a new focus for the ACT. We at 36U have come up with a fun challenge to help you prepare for this new focus area–AND to give you a chance to win prizes!
The Problem
In a fountain, there are 1,000 quarters, 2,000 dimes, 2,000 nickels, and 5,000 pennies. A student randomly draws a coin from the fountain each day for 3 years, records its value, and tosses it back into the fountain.
Let x equal the value of a coin drawn randomly from the fountain. If all coins are equally likely to be drawn, regardless of coin size, what is the expected value (long-run average) of x?
A. 1¢
B. 4¢
C. 6¢
D. 8¢
E. 10¢
How Do I Enter the Contest?
Take a pic of your solution, with your work included, and post as a reply to any of our Expected Value Fountain Challenge social media posts OR email to support@36university.com. Submissions must be posted by midnight eastern time on November 15th. Impress us with your easily-understood, clear solution!
What Will I Win?
The winner will receive the 36U Winter Care Package:
1 month access to 36U ACT Prep
36U Tee (Long-sleeve)
$15 Starbucks gift card
How Will 36U Choose a Winner?
At 36U, we value simple, precise solutions. We will draw a winner on November 16th from among entries with correct answers and easy-to-understand explanations. The winner’s submission will be included in our solution post.
New ACT Math Test Content Part 1: The Factorial
Combinatorics has been added to the ACT math test—and 36U is here to get you ready!
Don’t worry. Combinatorics may sound intimidating, but it’s really about fancy, advanced counting techniques that can be a lot of fun and save lots of time. Let’s get right to it.
Factorials
First, let’s work on a possibly new concept with some new notation—the factorial.
6 factorial, written 6!, means 6 • 5 • 4 • 3 • 2 • 1.
And, again:
5! = 5 • 4 • 3 • 2 • 1
To simplify, 5! = 5 • 4 • 3 • 2 • 1 = 120.
Let’s put the factorial to work…
Example 1: In how many different ways can you arrange the letters of the word OVERCAST?
____ ____ ____ ____ ____ ____ ____ ____
You have 8 options for the first letter, 7 options for the 2nd, 6 options for the 3rd, and so on.
Mathematically, that looks like this:
_8 options •_7 options •_6 options •_5 options •_4 options •_3 options •_2 options •_1 option
or
8! –> 40,320
There are 40,320 different ways the letters of OVERCAST can be arranged.
Easy so far. Let’s move on…
Example 2: In how many different ways can you arrange the letters of the word CANYON?
This is a slightly trickier item because CANYON has 2 N’s! Fortunately, if you understood our first example, this isn’t much more difficult.
Step 1: There are six different spots to place the letters in the word CANYON:
_6 options •_5 options •_4 options •_3 options •_2 options •_1 option = 6!
There are 6! or 720 different ways of arranging C-A-N-Y-O-N, but…You have to account for repeated options because there are 2 Ns. Here’s how:
Take your total number of possible arrangements (6!) and divide by 2! to account for N appearing twice.
6!/2! –> (6 • 5 • 4 • 3 • 2 • 1)/(2 • 1)
–> 360
There are 360 different ways the letters of the word CANYON can be arranged!
That’s your introduction to new counting techniques (combinatorics) that are being tested on the ACT.
Take time to brush up on your combination and permutations, too. For more instruction and practice on these topics, check out our online program.
-Dr. Kendal Shipley, 36U
10/13/17