Solution Page
The Locker Problem
 We want thank all who attempted the January 2017 Math Challenge. We hope you enjoyed and learned from the problem.
We want thank all who attempted the January 2017 Math Challenge. We hope you enjoyed and learned from the problem.
For those who missed it, here was the challenge problem:
Imagine 100 lockers numbered 1 to 100 with 100 students lined up in front of those 100 lockers:
The first student opens every locker.
The second student closes every 2nd locker.
The 3rd student changes every 3rd locker; if it’s closed, she opens it; if it’s open, she closes it.
The 4th student changes every fourth locker.
The 5th student changes every 5th locker.
That same pattern continues for all 100 students.
Here’s the question: “Which lockers are left open after all 100 students have walked the row of lockers?”
The Solution
As many of you found, the perfect square lockers (#s 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100) are the only lockers left open. Cool, huh?
We hope you realized that lockers are only touched by students who are factors of that locker number, i.e. locker #5 is only touched by students 1 and 5. Student 1 opens it and student 5 closes it. In fact, because factors come in pairs, the first student factor will open it and the corresponding factor student closes it. At first, maybe you thought every locker would be closed because factors come in pairs. But there was a twist…
Here are a couple of ways you could have gotten there:
Method 1: Solve a Simpler Problem
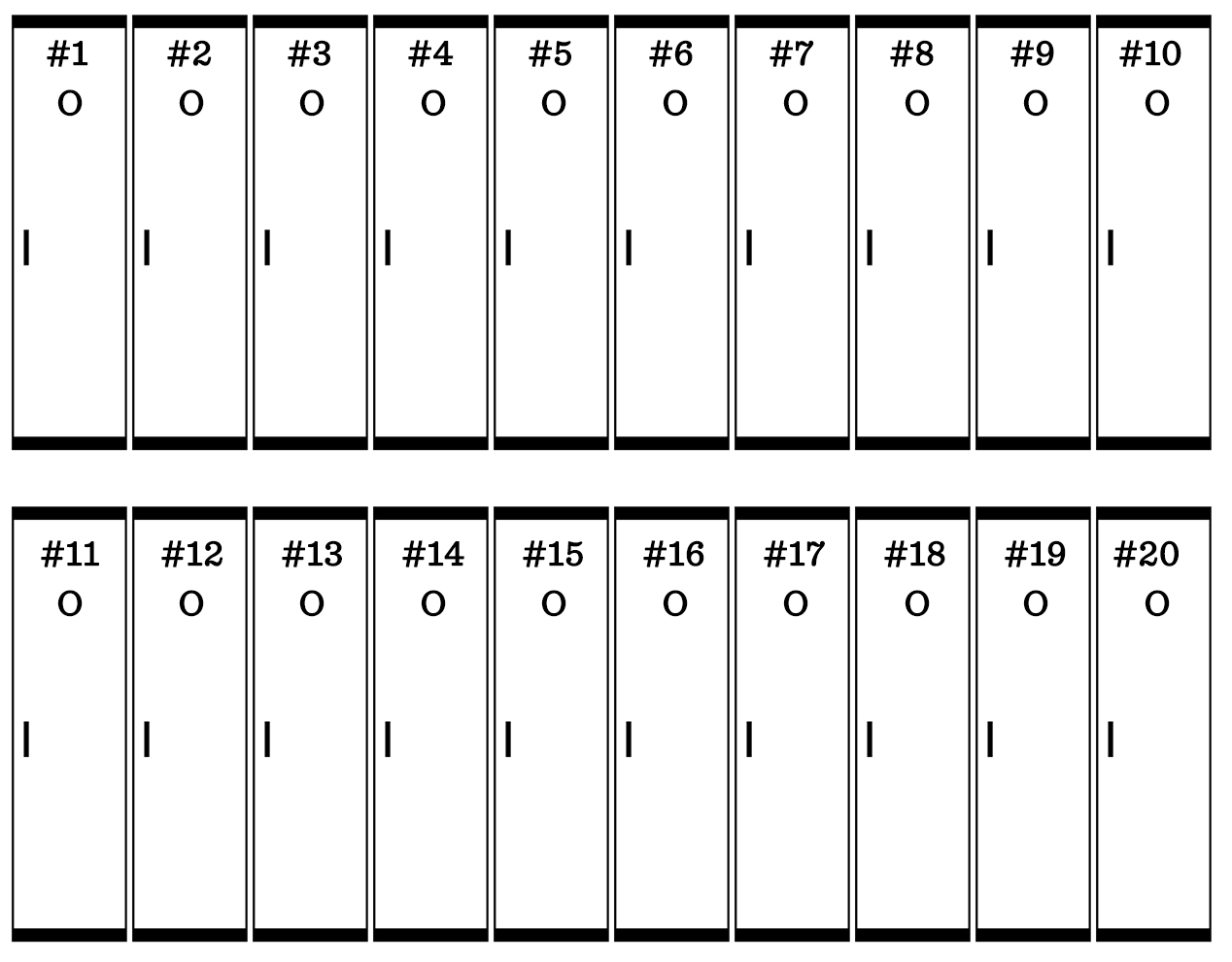
Start with just 20 lockers and try to find a pattern.
We used a code: O = Open, C = Closed.
Here’s what the lockers look like after the first student walks through. They are all open.
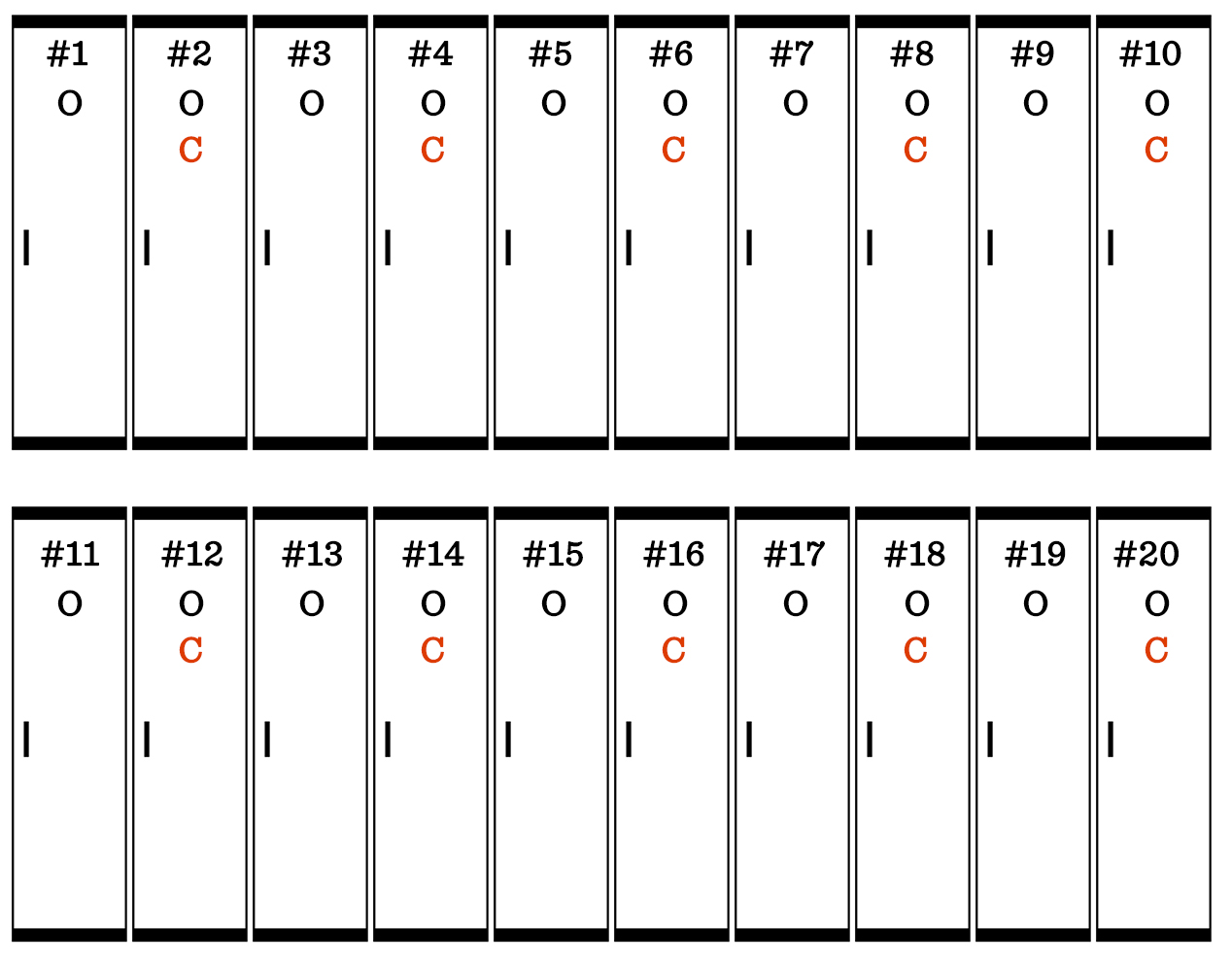
After the second student walks the row of lockers, the odd-numbered lockers are left open and the even-numbered lockers are closed:
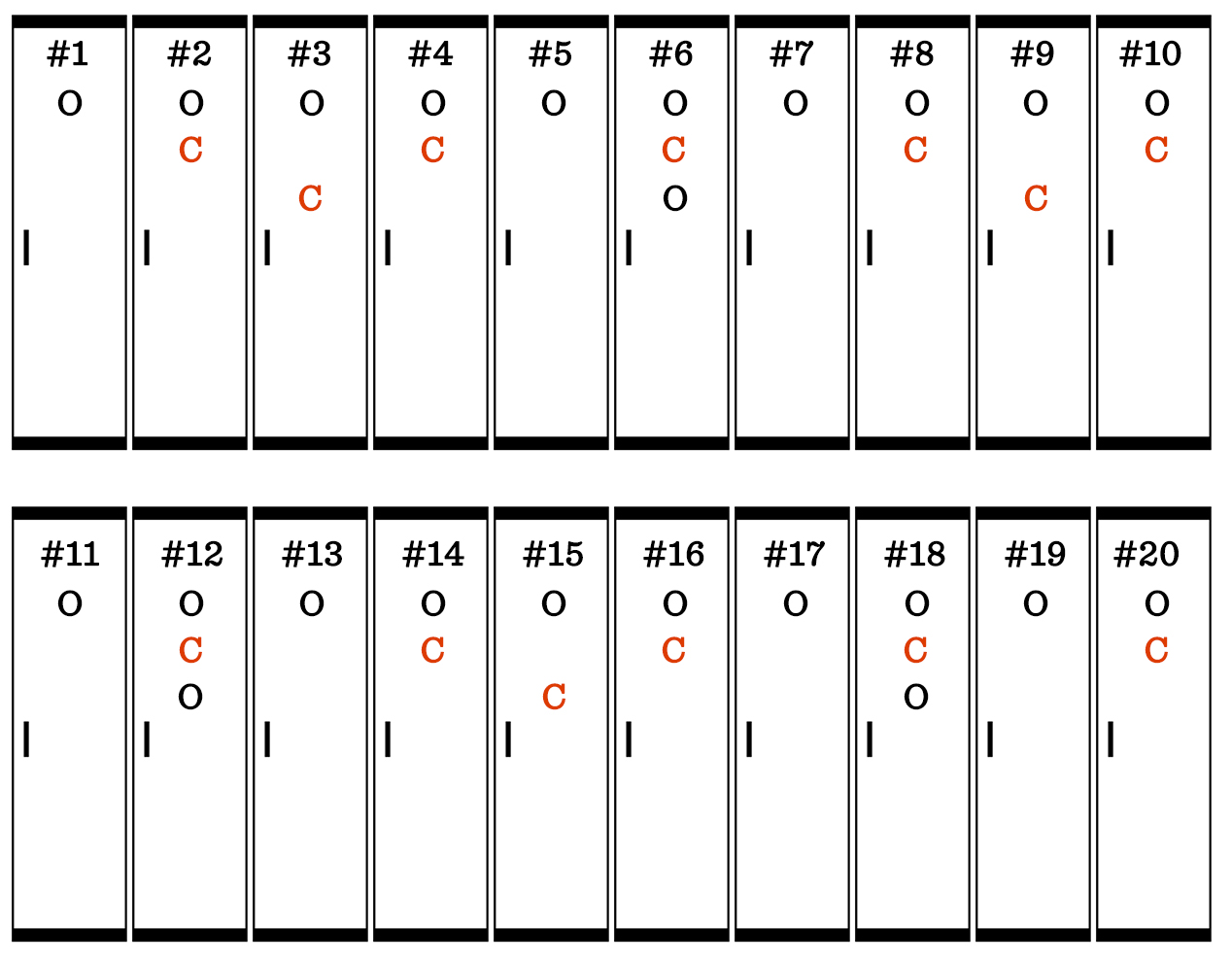
Here’s how the lockers look after the third student changes every 3rd locker:
And here’s how it looks after the first 20 students have walked the row of lockers. Note: after student 20 has gone, the first 20 lockers aren’t touched again.
Of the first 20 lockers, locker #s 1, 4, 9, and 16 are left open. Those are perfect squares. You can extend that pattern to identify the remaining open lockers.
Lockers 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are left open!
Method 2: Who Touches Which Lockers
Identifying which students touch which lockers is a little less of a brute-force approach and would likely have gotten you to the solution a little more quickly.
Here’s what I mean:
Consider locker #1. The only student who touches locker #1 is student #1. Student 1 opens the locker, and since no one else touches it, it will be left open at the end.
Consider locker #2. Student 1 opens the locker, and student 2 closes it. No one else touches the locker, so it will be closed.
Consider locker #10. Students 1 opens the locker. Student 2 closes it. Students 3 and 4 skip right by it. Student 5 opens it. Students 6, 7, 8, and 9 skip right by it. And student 10 closes it. Locker #10 will be closed.
Mental Milestone 1: After looking at several lockers, you should notice that lockers are only changed by student numbers that are factors of the locker number. In other words, locker 12 is changed by students 1, 2, 3, 4, 6, and 12.
Mental Milestone 2: You should also have noticed that factors always come in pairs. This means that for every student who opens a locker, there is another student who closes it. For locker #12, student 1 opens it, but student 12 closes it later. Student 2 opens it, but student 6 closes it later. Student 3 opens it, but student 4 closes it later.
By this logic, every locker would be closed.
But there are exceptions!
Consider locker #25. Student 1 opens it. Student 5 closes it. Student 25 opens it. The locker will be left open, but why? In this case, the factors do not come in pairs. One and 25 are a pair, but five times five is also 25. Five only counts as one factor. This causes the open-close pattern to be thrown off. Locker #25 is left open.
Mental Milestone 3: When factors don’t come in pairs, the locker will be left open. And factors don’t come in pairs when numbers are multiplied by themselves. Perfect squares (1, 4, 9, 16, 25, 36, 49, 64, 81, 100,…) are the only numbers whose factors don’t come in pairs because one set of factors, the square root, is multiplied by itself. This means that only perfect square lockers will be left open.
Locker #s 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are left open!
The Winner
Congratulations to Sydney H, our January 2017 ACT Challenge winner! Her solution was simple, precise, and just as important, correct. In fact, I like her solution better than the explanations I provided above. Here’s what she had to say:
Sydney won the 36U Winter Care Package:
3 months access to 36U ACT Prep
36U Tee (Long-sleeve)
36U toboggan
$15 Starbucks gift card
More 36U Resources: