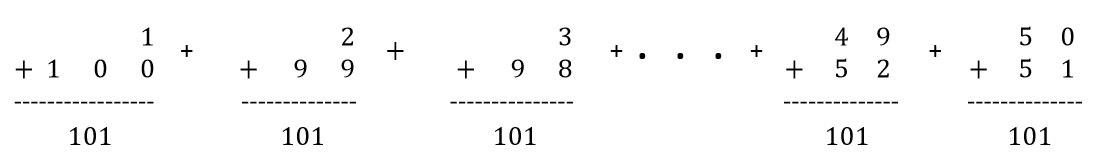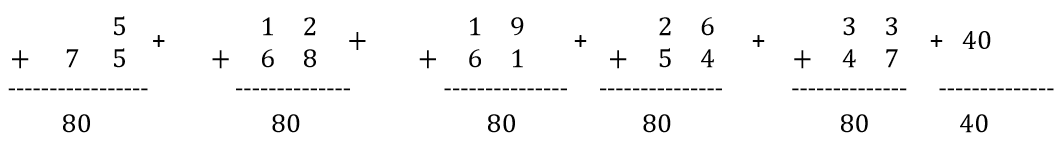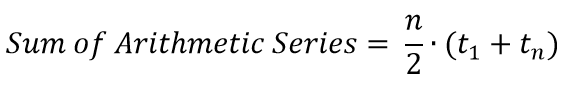The Story of Lil Carl and the Arithmetic Series
Lil Carl bounced into kindergarten on a warm spring morning– energetic, but bored. Not one thing Ms. Artwaller had thrown at him that year had come close to testing his abilities. Exasperated Ms. Artwaller had had enough of Lil Carl disrupting class and decided to put an end to his shenanigans. “Find the sum of the first 100 whole numbers,” she said. At long last, Ms. Artwaller was finally able to teach the class without Lil Carl doing Lil Carl things…
After just a few moments Lil Carl was back: “5050. You did want me to add whole numbers 1 to 100, right?”
(This story is based on a legendary tale of one of the greatest mathematicians of the 18th and 19th centuries, Carl Friedrich Gauss. Read more here.)
How Did He Do That?
Even though the numbers are sequentially 1, 2, 3, and so on, you don’t have to add them in that order. In fact, the addition is much quicker if you change the arrangement. Add 1 and 100; add 2 and 99; continue with that pattern.
Step 1: Wrap the second half of the series below the first half, and then add.
Now, we have a bunch of 101s. In fact, we have 50 of them. So, instead of adding 100 terms, we can now multiply!
Step 2: Multiply!
We have fifty 101s now, so multiply:
50 • 101 –> 5050
The sum of 1 + 2 + 3 + … + 100 is 5050. We folded the series in half, so that we added the first half of the series with the second half of the series. This eventually allowed us to multiply to get the sum of the series.
What about Other Arithmetic Series?
Suppose we wanted to add 5 + 12 + 19 + … + 75. (Hint: The difference between consecutive terms is 7.)
Step 1: Fold the series in half.
Step 2: Find the number of terms after the series is folded in half.
a. From the first term of 5 to the last term of 75 is a jump of 70.
b. The jump between each term is 7, so there are 10 total jumps.
c. There are 11 terms in the original series of 5 + 12 + 19 + … + 75. (10 jumps and the first term)
d. After the series is folded in half, there will be five full pairs and an odd term in the middle without a pair. We will call that 5 ½ pairs.
Step 3: Multiply!
The pairs add to 80. There are 5.5 pairs.
80 • 5.5 –> 440
Arithmetic Series Formula
Arithmetic series can always be added with the method shared above. If had rather use a formula, however, here it is:
where n = # of terms in the series, t1 is the first term in the series, and tn is the last term in the series.
Please note: The formula mirrors the method used above. The first and last terms are added (t1 + tn) and then multiplied by half of the number of terms in the series (n/2).
How Will This Look on the ACT?
Try this example from the 2014-2015 Preparing-for-the-ACT Guide (property of ACT Inc). If needed, start by writing out the terms in the sequence.
Recent and Related Posts
#1 Skill Needed to Score Well on the ACT May Be Reading Comprehension
Get a Copy of Your ACT and Fix the Mistakes