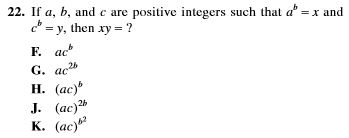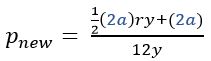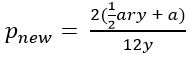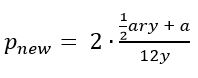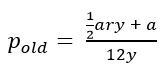The Six Trickiest Math Problems We Found on the Most Recent ACT
The Six Trickiest Math Problems We Found on the Most Recent ACT
If you learned what your teachers taught in your math classes, then you should do great on the ACT math test. However, like most standardized tests, the ACT will throw a few items your way that look a little different than the items your teacher assigned.
So, here are the tricky items we found on the latest publicly-released ACT. There are six of them. Have questions or comments? Let us know! Please note: these aren’t necessarily the most difficult items on the math test, though some are, but they are the ones that we consider the slyest.
All items shown below are from the 2016-2017 Preparing-for-the-ACT Guide. They are the property of ACT Inc., not 36 University.
What’s Tricky About It?
This item is asking for an application of an exponents rule, but in a way that isn’t usually stressed in math classrooms. Usually, students are taught to distribute exponents to the bases:
(ab)x –> axbx
But this problem asks students to apply the same concept, but in reverse.
How You Should Work It
The problem asks for x•y.
Step 1) Use the information from the problem (x = ab and y =cb) to substitute for x and y.
x•y –> abcb
Step 2) Apply the exponent rule (ab)x –> axbx in reverse. In other words, both bases have the same exponent, so the exponent can be placed outside parentheses:
abcb –> (ac)b
The answer is H.
What’s Tricky About It?
Monthly payment. P dollars. Short-term loan. Annual interest rate. This item is wordy, and the vocabulary is a little tough. On top of that, that equation is intimidating.
On top of that, many students won’t know how to handle multiplying a by 2.
How You Should Work It
Step 1) Multiply a by 2.
Here’s the new value for p:
Step 2) Factor out the 2.
Don’t make this too complicated: use the distributive property in reverse.
and because multiplying the numerator by 2 is the same as multiplying the fraction by 2:
Step 3) Compare to the previous value for p.
In the problem, the value for p was:
When a is multiplied by 2, p is also multiplied by 2. The answer is D.
What’s Tricky About It?
Reasoning through this item, especially with its fractions, is very difficult. Only the top students may find that a navigable path.
How You Should Work It
The easiest way to work the item is to set up an equation that mirrors the situation.
Let x = volume of the container in cups
Step 1) Set up the equation.
The problem says they took 1/8 of the container, added 10 cups, and ended with the container 3/4 full. Or, maybe this is simpler: One-eighth of the container plus 10 cups equals three-fourths of the container.
As an equation, that description looks like this:
Step 2) Solve the equation for x, the volume of the container.
Subtract (1/8)*x from both sides.
Multiply both sides of the equation by 8/5.
x = 16 cups
The answer is J.
It’s also a good practice to check your solution with the information given in the problem. Have fun!
What’s Tricky About It?
Students are often more comfortable working from point A to point B along a path they’ve trod several times before. This item invites students to reason to try to find the relationship between x and z, but that reasoning is difficult.
How You Should Work It
There is a variable common in both ratios—y. Rewrite both ratios so that y has the same value in both.
Step 1) Rewrite both ratios.
The variable y corresponds with the 2 in the first ratio and a 3 in the second ratio. Rewrite both ratios so that y has a value of 6 (least common multiple).
and
Step 2) Make the comparison between x and z.
Rewriting both ratios as fractions with a y value of 6 allows us to compare x and z.
If the ratio of x to y is 15 to 6 and the ratio of y to z is 6 to 4, then the ratio of x to z is 15 to 4.
The answer is E.
What’s Tricky About It?
This item, like a few others in this list, is likely to have students spending an inordinate amount of time with a trial-and-error method trying reason their way to the answer. That is a tough road!
How You Should Work It
Students need a Venn Diagram in their math tool chest. Unfortunately, many of them may not have used a Venn Diagram since the 8th grade.
Set up a Venn Diagram for all 120 students.
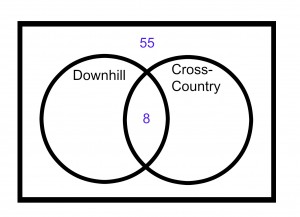
Step 1) Survey question one tells us that 55 students have neither skied cross-country or downhill.
Step 2) Use survey questions two and three to find the number of students who have skied both cross-country and downhill.
Survey question one states that 65 students have either skied cross-country or downhill. Survey question two states that 28 have skied downhill and 45 have skied cross-country. That’s 73 total, 8 more than the 65 from Q1. That means some of them have done both!
Take the surplus of 8 and place them in the overlap for students who have skied both downhill and country-country.
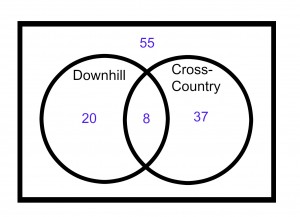
Step 3) Use survey questions 2 and 3 to finish out the Venn Diagram.
Twenty-eight students have skied downhill.
Forty-five students have skied cross-country.
Step 4) Check your Venn Diagram with the original information.
After your check, you’ll see that indeed 8 of the students had skied both cross-country and downhill.
The answer is E.
What’s Tricky About It?
There are two difficulties here:
1) Rate problems are standard fare in algebra class, but this item isn’t worked like most of those textbook problems are worked.
2) The wording is strange. Who ever asks about how many cans of food a dog eats in “’3 + d days?’”
How You Should Work It
Step 1) Recognize the rate at which the dog is eating.
Seven cans in three days means the dog is eating 7/3 of a can per day. This means that you can take the rate (7/3 of can per day) and multiply by the number of days to get the total amount of dog food consumed.
Try this: After 3 days the dog has eaten (7/3) * 3 = 7 cans of food, just like the problem stated.
Step 2) Substitute to find the solution.
How many cans does the dog eat in 3 + d days? Break this into two separate parts. In 3 days, the dog eats 7 cans, just like the problem told us. In d days, the dog eats (7/3)*d cans, just like we figured in Step 1. This means the dog eats 7 + (7/3)*d cans.
The answer is K.