THE Problem I Missed on the ACT Math Test
The original title of this post was supposed to be “The Math Problem I Had to Skip and Come Back To,” but it didn’t work out that way. I formulated the first title after I had to skip THE problem the first time.
I ended up missing the problem!
Recently, ACT Inc put out a new “Official ACT Prep Guide” and, as I always do, I sat down to take the tests (timed, of course) and to categorize the new items. This time, I set the timer and began working.
I was halfway through at the 19-minute mark and had no troubles. I noticed the problems were taking me a little more time than I wanted, but I only had a phone calculator and was only willing to use a small notepad to write something down if absolutely necessary.
No problems so far.
And then I hit #51:
(This item is owned by ACT Inc and printed in the first practice test in The Official ACT Practice Guide 2016-2017.)
I made a mental list of all possible perfect square sums from students 1 through 18: 4, 9, 16, 25. I started working and realized I couldn’t see the “quick way.”
Yes, almost all ACT Math items have a “quick way.” So, contrary to what I think most students should do at this point (which is to give it their best guess and move on), I skipped it.
I made my way through the rest of the test. The dumb “how many quarters are there?” problem. The Venn diagram problem. The Law of Sines. A probability distribution (That’s new!). And I headed back to #51…
I had about 4 minutes left at this point and decided to continue with the the brute force approach (another critical error?).
I eliminated choices A and C, because 1 + 16 and 1 + 9 don’t give perfect squares.
A little more deduction told me 17 had to be be paired with 8 to give the perfect square 25. Student 17 had to be paired with another student to give a perfect square. There wasn’t a student who could pair with 17 to reach the perfect square 36 (17 + 18 = 35). There was no way to pair student 17 with another student and get a number less than 17, so the only option was to add to 25. That made student 17 pair with student 8.
I was left with choices B and E.
I knew that 1 had to be paired with 3 or 15 (I had known that since the first pass through.). I scribbled. I paired. I scribbled. I paired.
And I still didn’t get it. I was running out of time! I chose…3.
Wrong choice!
What Did I Do Wrong?
I’m not really sure where I went wrong. Is there a key that unlocks this problem quickly? I don’t know.
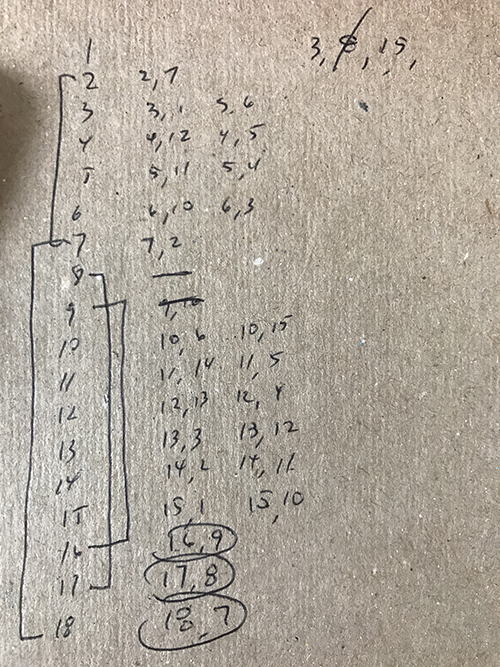
Eventually, I did figure that 1 had to be paired with 15, and this is how I did it…
Step 1: Start with the big numbers.
Pair student 18 with student 7, which is the only option for reaching a perfect square. Likewise, student 17 has to be paired with student 8. Student 16 has to be paired with student 9. Of the nine pairs, we have 3 pairs figured quickly!
Student 15 can be paired with student 10 (sum of 25) or student 1 (sum of 16).
Student 14 can be paired with student 11 (sum of 25) or student 2 (sum of 16).
Student 13 can be paired with student 12 (sum of 25) or student 3 (sum of 16).
Student 12 can be paired with student 13 (sum of 25) or student 4 (sum of 16).
Student 11 can be paired with student 14 (sum of 25) or student 5 (sum of 16).
Student 10 can be paired with student 15 (sum of 25) or student 6 (sum of 16).
Student 9 is already paired with student 16 (see above).
Student 8 is already paired with student 17 (see above).
Student 7 is already paired with student 18 (see above).
Student 6 can be paired with student 10 (sum of 16) or student 3 (sum of 9).
Student 5 can be paired with student 11 (sum of 16) or student 4 (sum of 9).
Student 4 can be paired with student 12 (sum of 16) or student 5 (sum of 9).
Student 3 can be paired with student 13 (sum of 16) or student 6 (sum of 9) or student 1 (sum of 4).
Student 2 can be paired with student 14 (sum of 16), not student 7 (already paired with student 18), not student 2, because he is student 2. We have our fourth pair! Student 2 is paired with student 14!
Student 1 can be paired with student 15 (sum of 16) not student 8 (already paired with student 17) or student 3 (sum of 4).
Step 2: Student 2 is the key.
Student 2 is paired with student 14. From there, work backwards from student to student eliminating possible choices until student 1’s pair is identified.
Go to the Student 14 line. Student 14 is paired with student 2, so that leaves student 11.
Student 11 can’t be paired with student 14. Student 11 is paired with student 5.
Student 5 is paired with student 11, so that leaves student 4.
Student 4 must be paired with student 12.
Student 12 is paired with 4. That leaves student 13.
Student 13 is paired with student 3. The leaves students 1 and 6.
Student 6 is paired with student 10, because student 3 is paired with student 3.
Student 10 is paired with student 6. That leaves student 15.
Student 15 must be paired with student 1!!!
Is there a better way?
For a 60 second per item pace, ACT is asking a lot in this problem.
Do you see a more efficient way to work this problem? If so, tell me how in the comments below.
Kendal Shipley, Ed.D.
8/29/2017