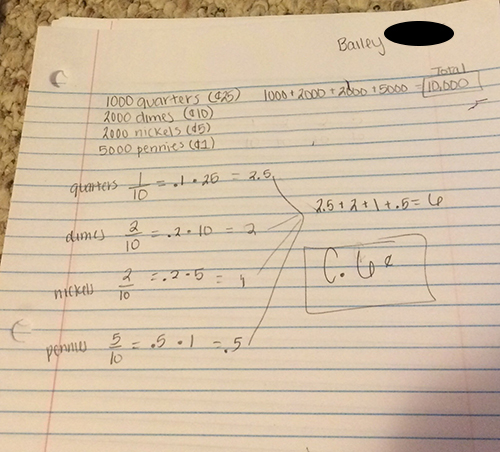Expected Value Challenge Item Winter Challenge
November 2018
Solution Page
 We at 36U want to thank the many students and teachers who participated in our November 2018 Winter Challenge. We hope you enjoyed working the item and learned a new skill or two along the way!
We at 36U want to thank the many students and teachers who participated in our November 2018 Winter Challenge. We hope you enjoyed working the item and learned a new skill or two along the way!
For those who missed it, here was the challenge problem:
The Problem
In a fountain, there are 1,000 quarters, 2,000 dimes, 2,000 nickels, and 5,000 pennies. A student randomly draws a coin from the fountain each day for 3 years, records its value, and tosses it back into the fountain.
Let x equal the value of a coin drawn randomly from the fountain. If all coins are equally likely to be drawn, regardless of coin size, what is the expected value (long-run average) of x?
A. 1¢
B. 4¢
C. 6¢
D. 8¢
E. 10¢
The Solution
The expected value, or long-run average, of coins drawn randomly from the fountain is 6 cents.
Almost every submission was correct. Great work!
Here’s how we worked the item:
Step 1: Find the probability of each outcome.
The first step in solving expected value items is to find the probability of each outcome. Often, the ACT will provide those probabilities in a probability distribution table.
Finding the probabilities will allow us to weight each outcome in Step 2.
Here’s the probability of each outcome:
P(penny) = 5,000 pennies/10,000 total coins = 1/2
P(nickel) = 2,000 nickels/10,000 total coins = 1/5
P(dime) = 2,000 dimes/10,000 total coins = 1/5
P(quarter) = 1,000 quarters/10,000 total coins = 1/10
Step 2: Weight each outcome.
Now that you know the probability of each outcome, weight each outcome value by multiplying by its probability.
One-half of the time, the student draws a penny that is worth 1 cent.
1/2 • 1¢ –> .5¢
One-fifth of the time, the student draws a nickel that is worth 5 cents.
1/5 • 5¢ –> 1¢
One-fifth of the time, the student draws a dime that is worth 10 cents.
1/5 • 10¢ –> 2¢
One-tenth of the time, the student draws a quarter that is worth 25 cents.
1/10 • 25¢ –> 2.5¢
Step 3: Add the values.
The probabilities add to 1. When we multiplied the probabilites by the values, we essentially broke down a single draw from the fountain into all the possible outcomes, weighted, of course.
Now it’s time to add those values to see what an average draw from the fountain would give.
Expected value = .5¢ + 1¢ + 1¢ + 2.5¢
Expected value = 6¢
The expected value, or long-run average, of a coin drawn randomly from the fountain is 6¢.
Impressive solution!
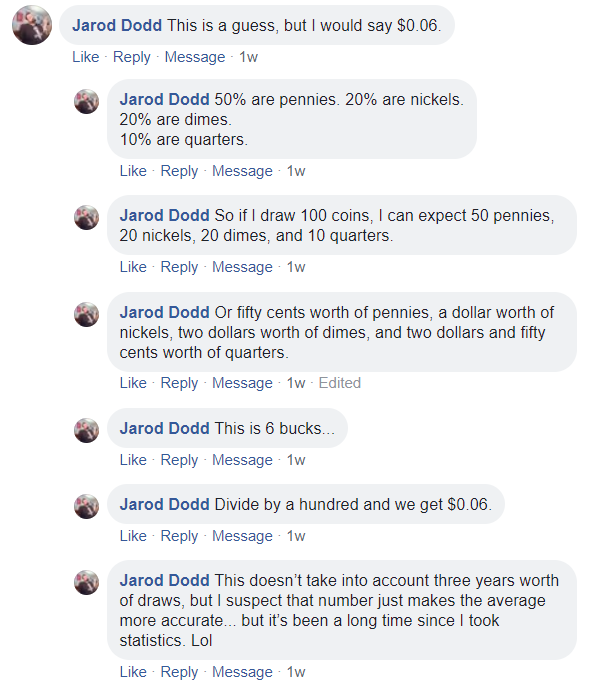
One of our favorite problem solving approaches came via Facebook. Check it out.
The Winner
Congratulations to Bailey S., our November 2018 Expected ValueChallenge winner! Her solution was simple, precise, and just as important, correct. Here’s what she had to say:
Bailey won the 36U Winter Care Package:
1 month of access to 36U ACT Prep
36U Tee (Long-sleeve)
$15 Starbucks gift card