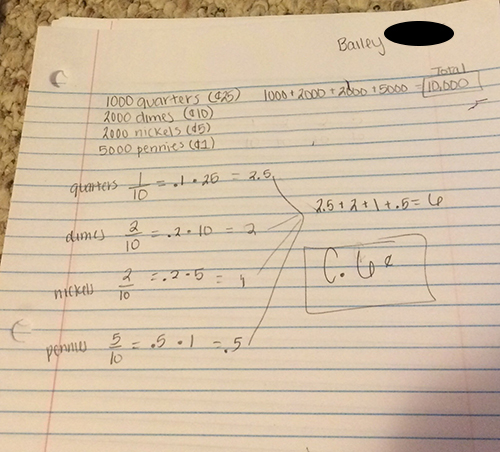Expected Value Challenge Item Winter Challenge
November 2018
Solution Page
We at 36U want to thank the many students and teachers who participated in our November 2018 Winter Challenge. We hope you enjoyed working the item and learned a new skill or two along the way!
For those who missed it, here was the challenge problem:
The Problem
In a fountain, there are 1,000 quarters, 2,000 dimes, 2,000 nickels, and 5,000 pennies. A student randomly draws a coin from the fountain each day for 3 years, records its value, and tosses it back into the fountain.
Let x equal the value of a coin drawn randomly from the fountain. If all coins are equally likely to be drawn, regardless of coin size, what is the expected value (long-run average) of x?
A. 1¢
B. 4¢
C. 6¢
D. 8¢
E. 10¢
The Solution
The expected value, or long-run average, of coins drawn randomly from the fountain is 6 cents.
Almost every submission was correct. Great work!
Here’s how we worked the item:
Step 1: Find the probability of each outcome.
The first step in solving expected value items is to find the probability of each outcome. Often, the ACT will provide those probabilities in a probability distribution table.
Finding the probabilities will allow us to weight each outcome in Step 2.
Here’s the probability of each outcome:
P(penny) = 5,000 pennies/10,000 total coins = 1/2
P(nickel) = 2,000 nickels/10,000 total coins = 1/5
P(dime) = 2,000 dimes/10,000 total coins = 1/5
P(quarter) = 1,000 quarters/10,000 total coins = 1/10
Step 2: Weight each outcome.
Now that you know the probability of each outcome, weight each outcome value by multiplying by its probability.
One-half of the time, the student draws a penny that is worth 1 cent.
1/2 • 1¢ –> .5¢
One-fifth of the time, the student draws a nickel that is worth 5 cents.
1/5 • 5¢ –> 1¢
One-fifth of the time, the student draws a dime that is worth 10 cents.
1/5 • 10¢ –> 2¢
One-tenth of the time, the student draws a quarter that is worth 25 cents.
1/10 • 25¢ –> 2.5¢
Step 3: Add the values.
The probabilities add to 1. When we multiplied the probabilites by the values, we essentially broke down a single draw from the fountain into all the possible outcomes, weighted, of course.
Now it’s time to add those values to see what an average draw from the fountain would give.
Expected value = .5¢ + 1¢ + 1¢ + 2.5¢
Expected value = 6¢
The expected value, or long-run average, of a coin drawn randomly from the fountain is 6¢.
Impressive solution!
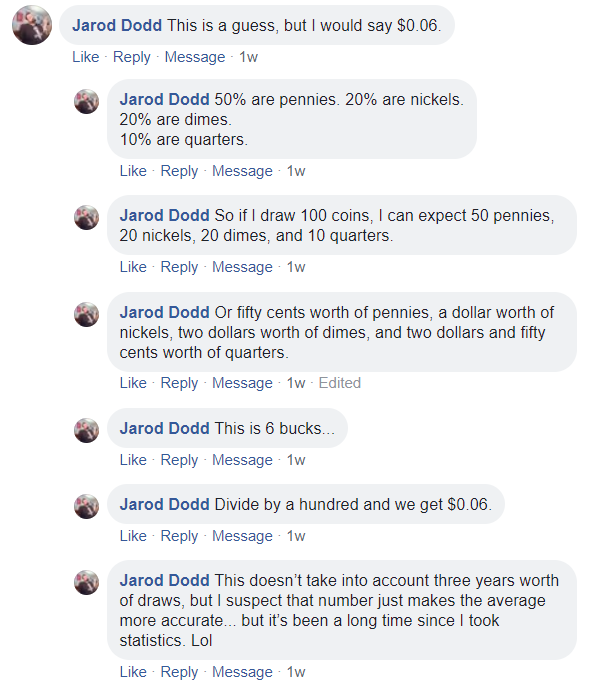
One of our favorite problem solving approaches came via Facebook. Check it out.
The Winner
Congratulations to Bailey S., our November 2018 Expected ValueChallenge winner! Her solution was simple, precise, and just as important, correct. Here’s what she had to say:
The Winnings!
Bailey won the 36U Winter Care Package:
1 month of access to 36U ACT Prep
36U Tee (Long-sleeve)
$15 Starbucks gift card
Expected Value Challenge Item Giveaway
November 2018
Statistics and probability are a new focus for the ACT. We at 36U have come up with a fun challenge to help you prepare for this new focus area–AND to give you a chance to win prizes!
The Problem
In a fountain, there are 1,000 quarters, 2,000 dimes, 2,000 nickels, and 5,000 pennies. A student randomly draws a coin from the fountain each day for 3 years, records its value, and tosses it back into the fountain.
Let x equal the value of a coin drawn randomly from the fountain. If all coins are equally likely to be drawn, regardless of coin size, what is the expected value (long-run average) of x?
A. 1¢
B. 4¢
C. 6¢
D. 8¢
E. 10¢
How Do I Enter the Contest?
Take a pic of your solution, with your work included, and post as a reply to any of our Expected Value Fountain Challenge social media posts OR email to support@36university.com. Submissions must be posted by midnight eastern time on November 15th. Impress us with your easily-understood, clear solution!
What Will I Win?
The winner will receive the 36U Winter Care Package:
1 month access to 36U ACT Prep
36U Tee (Long-sleeve)
$15 Starbucks gift card
How Will 36U Choose a Winner?
At 36U, we value simple, precise solutions. We will draw a winner on November 16th from among entries with correct answers and easy-to-understand explanations. The winner’s submission will be included in our solution post.
Solution Page
The Locker Problem
We want thank all who attempted the January 2017 Math Challenge. We hope you enjoyed and learned from the problem.
For those who missed it, here was the challenge problem:
Imagine 100 lockers numbered 1 to 100 with 100 students lined up in front of those 100 lockers:
The first student opens every locker.
The second student closes every 2nd locker.
The 3rd student changes every 3rd locker; if it’s closed, she opens it; if it’s open, she closes it.
The 4th student changes every fourth locker.
The 5th student changes every 5th locker.
That same pattern continues for all 100 students.
Here’s the question: “Which lockers are left open after all 100 students have walked the row of lockers?”
The Solution
As many of you found, the perfect square lockers (#s 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100) are the only lockers left open. Cool, huh?
We hope you realized that lockers are only touched by students who are factors of that locker number, i.e. locker #5 is only touched by students 1 and 5. Student 1 opens it and student 5 closes it. In fact, because factors come in pairs, the first student factor will open it and the corresponding factor student closes it. At first, maybe you thought every locker would be closed because factors come in pairs. But there was a twist…
Here are a couple of ways you could have gotten there:
Method 1: Solve a Simpler Problem
Start with just 20 lockers and try to find a pattern.
We used a code: O = Open, C = Closed.
Here’s what the lockers look like after the first student walks through. They are all open.
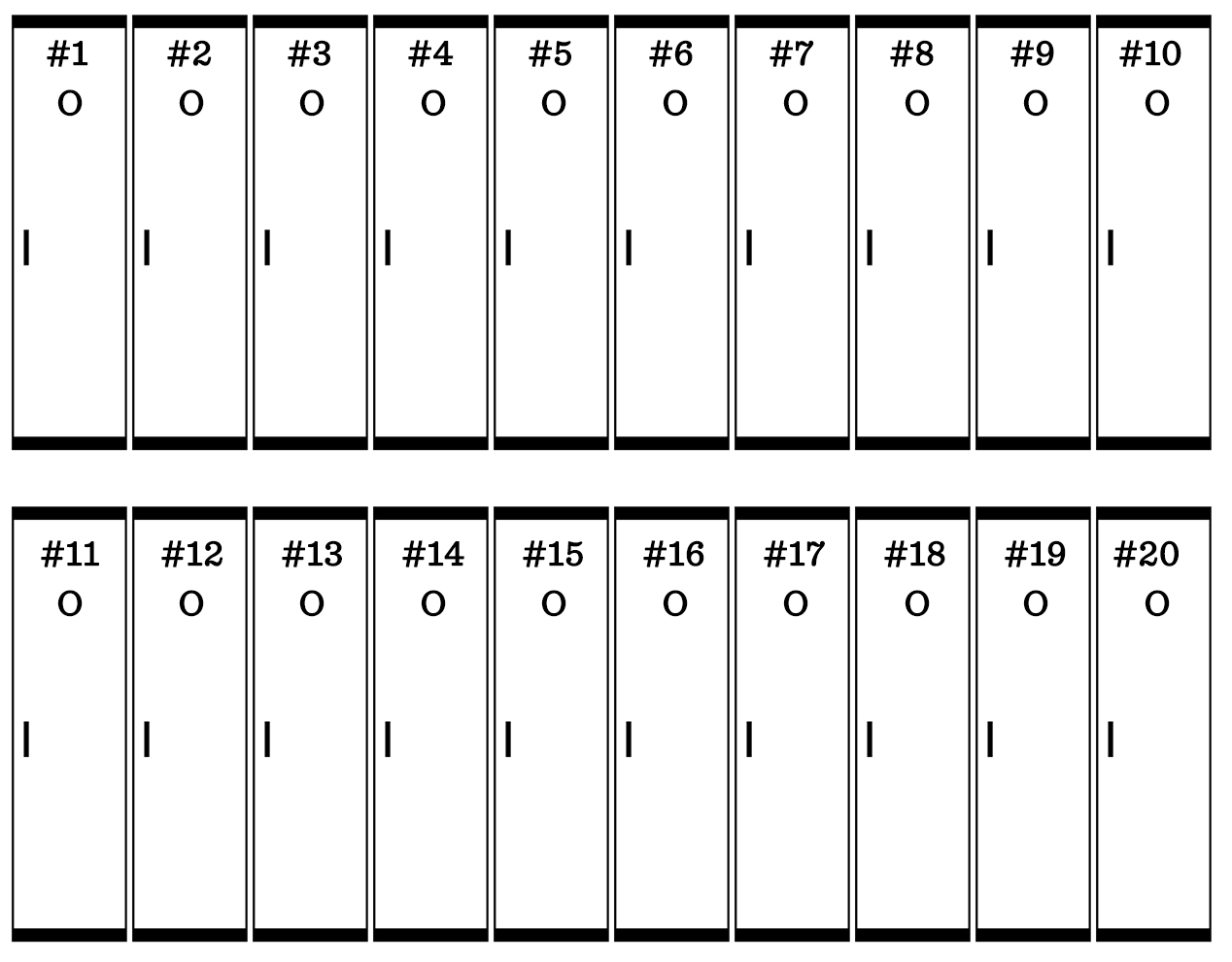
After the second student walks the row of lockers, the odd-numbered lockers are left open and the even-numbered lockers are closed:
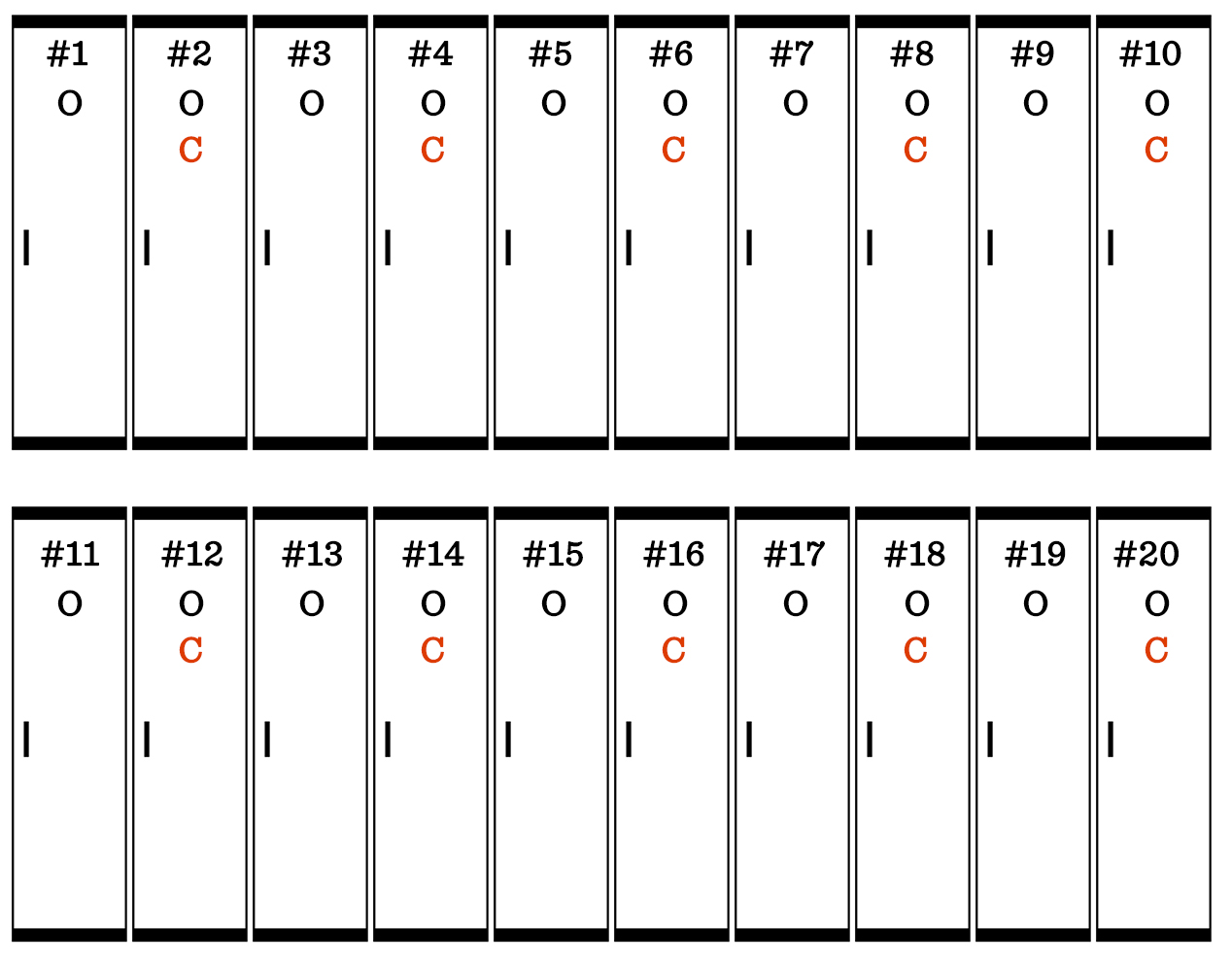
Here’s how the lockers look after the third student changes every 3rd locker:
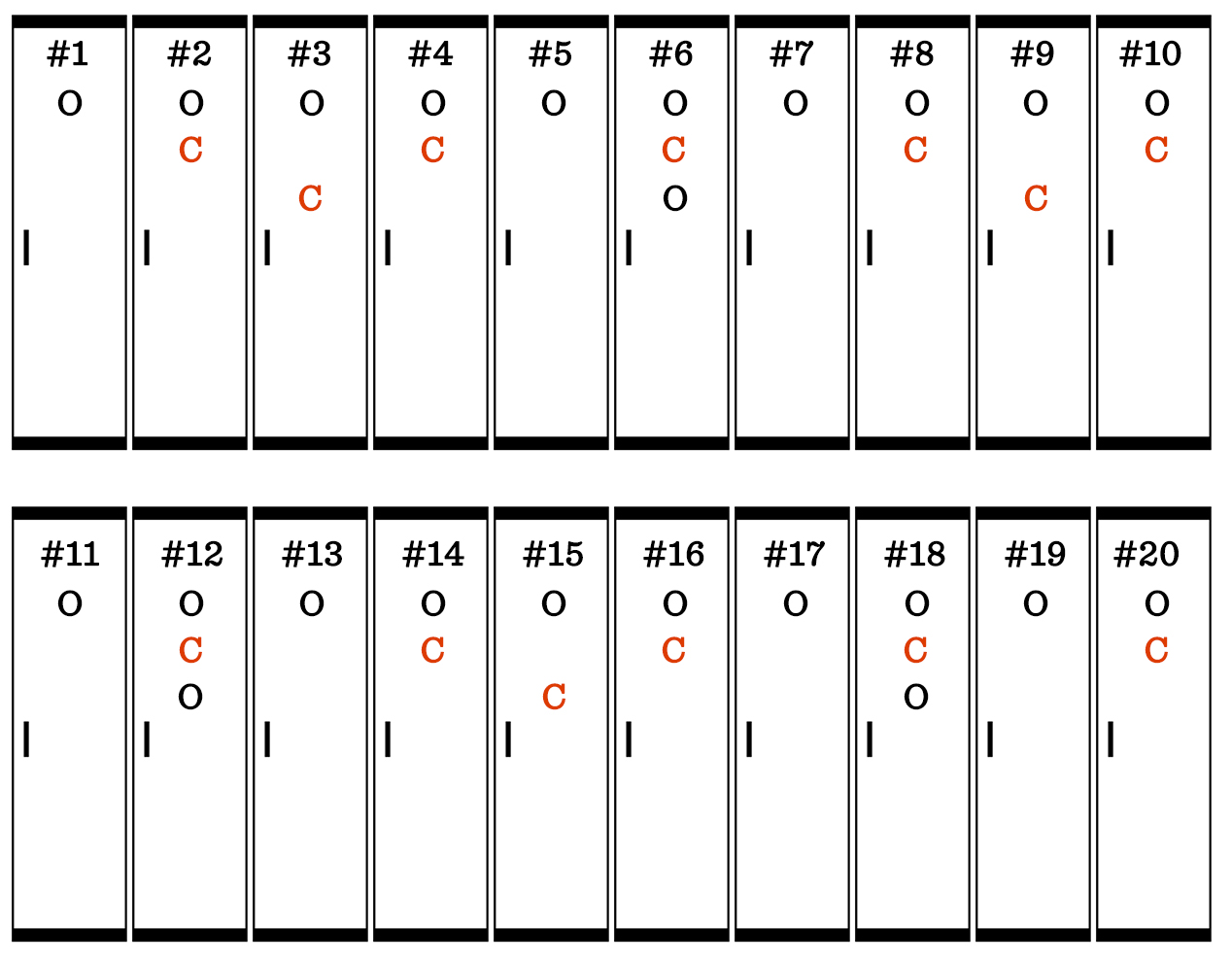
And here’s how it looks after the first 20 students have walked the row of lockers. Note: after student 20 has gone, the first 20 lockers aren’t touched again.
Of the first 20 lockers, locker #s 1, 4, 9, and 16 are left open. Those are perfect squares. You can extend that pattern to identify the remaining open lockers.
Lockers 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are left open!
Method 2: Who Touches Which Lockers
Identifying which students touch which lockers is a little less of a brute-force approach and would likely have gotten you to the solution a little more quickly.
Here’s what I mean:
Consider locker #1. The only student who touches locker #1 is student #1. Student 1 opens the locker, and since no one else touches it, it will be left open at the end.
Consider locker #2. Student 1 opens the locker, and student 2 closes it. No one else touches the locker, so it will be closed.
Consider locker #10. Students 1 opens the locker. Student 2 closes it. Students 3 and 4 skip right by it. Student 5 opens it. Students 6, 7, 8, and 9 skip right by it. And student 10 closes it. Locker #10 will be closed.
Mental Milestone 1: After looking at several lockers, you should notice that lockers are only changed by student numbers that are factors of the locker number. In other words, locker 12 is changed by students 1, 2, 3, 4, 6, and 12.
Mental Milestone 2: You should also have noticed that factors always come in pairs. This means that for every student who opens a locker, there is another student who closes it. For locker #12, student 1 opens it, but student 12 closes it later. Student 2 opens it, but student 6 closes it later. Student 3 opens it, but student 4 closes it later.
By this logic, every locker would be closed.
But there are exceptions!
Consider locker #25. Student 1 opens it. Student 5 closes it. Student 25 opens it. The locker will be left open, but why? In this case, the factors do not come in pairs. One and 25 are a pair, but five times five is also 25. Five only counts as one factor. This causes the open-close pattern to be thrown off. Locker #25 is left open.
Mental Milestone 3: When factors don’t come in pairs, the locker will be left open. And factors don’t come in pairs when numbers are multiplied by themselves. Perfect squares (1, 4, 9, 16, 25, 36, 49, 64, 81, 100,…) are the only numbers whose factors don’t come in pairs because one set of factors, the square root, is multiplied by itself. This means that only perfect square lockers will be left open.
Locker #s 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are left open!
The Winner
Congratulations to Sydney H, our January 2017 ACT Challenge winner! Her solution was simple, precise, and just as important, correct. In fact, I like her solution better than the explanations I provided above. Here’s what she had to say:
The Winnings!
Sydney won the 36U Winter Care Package:
3 months access to 36U ACT Prep
36U Tee (Long-sleeve)
36U toboggan
$15 Starbucks gift card
More 36U Resources:
36U Blog Posts
36U ACT Tips
36U ACT Prep Program
The Locker Problem – January 2017 Challenge
Number properties are rarely reviewed, but they are sometimes tested on the ACT. So, we’ve decided to share a fun, straightforward, and hopefully enlightening item that will have you thinking about number properties. Here’s your January 2017 ACT Math Challenge:
Imagine 100 lockers numbered 1 to 100 with 100 students lined up in front of those 100 lockers:
The first student opens every locker.
The second student closes every 2nd locker.
The 3rd student changes every 3rd locker; if it’s closed, she opens it; if it’s open, she closes it.
The 4th student changes every fourth locker.
The 5th student changes every 5th locker.
That same pattern continues for all 100 students.
Here’s the question: “Which lockers are left open after all 100 students have walked the row of lockers?”
How Do I Enter?
Take a pic of your solution, with your work included, and post as a reply to any of our Locker Problem social media posts or send to lockerchallenge@36university.com. Submissions must be posted by midnight eastern time on January 31st. Impress us with your approach to solving this problem!
What Will I Win?
The winner will receive the 36U Winter Care Package:
3 months access to 36U ACT Prep
36U Tee (Long-sleeve)
36U toboggan
$15 Starbucks gift card
How Will 36U Choose a Winner?
At 36U, we value simple, precise solutions. We will draw a winner on February 1st from among entries with correct answers and easy-to-understand explanations. (or: whose solutions are correct and whose approach is easily understood.)
More 36U Resources:
36U Blog Posts
36U ACT Tips
36U ACT Prep Program