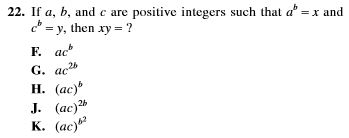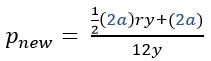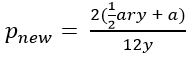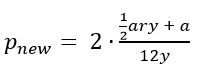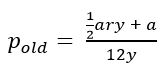New ACT Math Test Content Part 1: The Factorial
Combinatorics has been added to the ACT math test—and 36U is here to get you ready!
Don’t worry. Combinatorics may sound intimidating, but it’s really about fancy, advanced counting techniques that can be a lot of fun and save lots of time. Let’s get right to it.
Factorials
First, let’s work on a possibly new concept with some new notation—the factorial.
6 factorial, written 6!, means 6 • 5 • 4 • 3 • 2 • 1.
And, again:
5! = 5 • 4 • 3 • 2 • 1
To simplify, 5! = 5 • 4 • 3 • 2 • 1 = 120.
Let’s put the factorial to work…
Example 1: In how many different ways can you arrange the letters of the word OVERCAST?
____ ____ ____ ____ ____ ____ ____ ____
You have 8 options for the first letter, 7 options for the 2nd, 6 options for the 3rd, and so on.
Mathematically, that looks like this:
_8 options •_7 options •_6 options •_5 options •_4 options •_3 options •_2 options •_1 option
or
8! –> 40,320
There are 40,320 different ways the letters of OVERCAST can be arranged.
Easy so far. Let’s move on…
Example 2: In how many different ways can you arrange the letters of the word CANYON?
This is a slightly trickier item because CANYON has 2 N’s! Fortunately, if you understood our first example, this isn’t much more difficult.
Step 1: There are six different spots to place the letters in the word CANYON:
_6 options •_5 options •_4 options •_3 options •_2 options •_1 option = 6!
There are 6! or 720 different ways of arranging C-A-N-Y-O-N, but…You have to account for repeated options because there are 2 Ns. Here’s how:
Take your total number of possible arrangements (6!) and divide by 2! to account for N appearing twice.
6!/2! –> (6 • 5 • 4 • 3 • 2 • 1)/(2 • 1)
–> 360
There are 360 different ways the letters of the word CANYON can be arranged!
That’s your introduction to new counting techniques (combinatorics) that are being tested on the ACT.
Take time to brush up on your combination and permutations, too. For more instruction and practice on these topics, check out our online program.
-Dr. Kendal Shipley, 36U
10/13/17
Total Solar Eclipse: How to Plan
The Great American Solar Eclipse will happen in less than a week! August 21st is almost here!
We at 36U have been finalizing our plans for driving to the path of totality—and are excited about seeing the famous corona at full eclipse. We’ve decided where to go and we’ve gotten our eclipse glasses, so now it’s time for final plans.
What About the Weather?
First, we’re coming up with how we will handle the weather. What if it’s a cloudy—or even a rainy—day? We’ll be watching the forecast for our chosen site (almost two hours from home in the middle of the path of totality in Tennessee). I’ve decided that I’m going there no matter the weather, because part of what I want to experience is the darkness in the middle of the day, and that will happen rain or shine.
You might feel it’s better to stay home and watch live streaming or on television if a cloudy, rainy day is forecast. NASA will live stream in several different mediums. If you’re driving to the path of totality and can reach several different places, you might also change your destination based on a better forecast in another area.
Leave Early
But be aware that the prediction is for heavy traffic all around the path of totality throughout the U.S. One source estimates that over 7 million people will visit the path of totality. It’s likely that roads near the path will be very busy, and towns near interstates will perhaps be the most full. Some towns are charging $50 for a parking spot for viewing – and are almost sold out now.
Don’t wait any longer to make your plans!
The best strategy on eclipse day is to leave early and have plenty of extra time for reaching your destination. You don’t want your eclipse experience to be spent in the middle of a traffic jam!
Food and Drinks!
Since you’re planning for about three hours of eclipse time from beginning to end, take plenty of water or soft drinks, as well as plenty of snacks. The total eclipse near us is around lunch time, so we’re taking a picnic. We found a church that is letting us watch from its parking lot. We found it through an internet search of churches in an area not near the interstates. A phone call was all it took to get permission to view the eclipse from the parking lot. We will make a donation to that church, because we know many places have made the eclipse a money maker, and we appreciate the willingness to let us watch from church property.
Don’t Rely on Your Cell Phone
We have our eclipse glasses ready and will be printing or sending directions to our phone. Predictions are that cell towers may be overwhelmed with so many people communicating and using social media during the eclipse, so we’re making sure to have all of the information we need in case we don’t have to access the internet or map services. We will also take chairs and a big umbrella for shade so we’ll be comfortable for the three or more hours outside.
And, finally, sunscreen is a high priority because we’re hoping for a clear, sunny day to see what is a once-in-a-lifetime experience for most people!
We hope you have a good solar eclipse viewing experience, whether it’s in-person in the path of totality or online or on TV. Seeing the corona in a photo or video is pretty spectacular—and in person is that much better!
Happy viewing!
Krista Seckinger
36U Marketing Director
8/15/2017
Total Solar Eclipse Part 1: Where Do I Go?
Total Solar Eclipse Part 2: What Do I Need?
Total Solar Eclipse Part 3: How to Plan
36U Blog Posts
Total Solar Eclipse: What Do I Need?
The Great American Solar Eclipse is less than two weeks away!
Monday, August 21st will be here soon. If you’re in the path of totality (as we explained in our last blog post) or near it, it’s time to start thinking about what you need for your best eclipse viewing experience.
You probably already know you’re not supposed to look directly at the full or partially-eclipsed sun with the naked eye. So that you can watch the eclipse as it progresses, get eclipse-viewing glasses with NASA-recommended ISO 12312-2. Regular sunglasses are NOT safe for eclipse viewing. NASA has specific tips here to help you be safe while enjoying your eclipse viewing.
Of course, you might find some eclipse glasses that don’t seem to meet the ISO standard. The Washington Post, in this article, sums up the test to see if yours are okay: “When you look through them, you shouldn’t be able to see anything but the sun. Not the lights in your house, not the headlights on the street. Nothing but the sun.”
This same article goes on to list places carrying eclipse glasses. You can find them at retail stores such as Lowe’s, Walmart, Toys “R” Us, and Kroger, as well as convenience stores such as 7-Eleven, Circle K, Love’s Travel Stops, and Pilot/Flying J. A more comprehensive list is in the article. Some public libraries and other public organizations have free eclipse glasses, so it’s worth an internet search to see if any place near you is giving them away.
We at 36U have found it’s too late to order online and receive delivery by the eclipse date, so your best bet now is to find a free source locally or go to a local store. We even found empty eclipse glasses displays locally. So you may have to go on a hunt (as we did) to find your glasses before the 21st!
We know a lot of you will want to try some photos of the eclipse on your phone. Here’s some advice from Mr. Eclipse on how to do that.
If you want to try an “old school” DIY viewing method, there’s always the pinhole viewer. National Geographic gives an easy version: “Make a simpler version of the solar eclipse viewer with two thin but stiff pieces of white cardboard. Punch a small, clean pinhole in one piece of cardboard and let the sunlight fall through that hole onto the second piece of cardboard, which serves as a screen, held below it. An inverted image of the sun is formed. To make the image larger, move the screen farther from the pinhole. To make the image brighter, move the screen closer to the pinhole. Do not make the pinhole wide or you will only have a shaft of sunlight rather than an image of the crescent sun. Remember, this instrument is used with your back to the sun. The sunlight passes over your shoulder, through the pinhole, and forms an image on the cardboard screen beneath it. Do not look through the pinhole at the sun.”
Finally, don’t forget plenty of water and sunscreen and whatever you need to entertain yourself during the two-and-a-half to around three hours that it will take for the eclipse to run its whole course from beginning to end.
Happy viewing!
Total Solar Eclipse Part 1: Where Do I Go?
Total Solar Eclipse Part 2: What Do I Need?
Total Solar Eclipse Part 3: How to Plan
36U Blog Posts
Total Solar Eclipse: Where Do I Go?
You’ve probably heard by now that a solar eclipse will be sweeping across a swath of the United States on Monday, August 21st. We at 36U are excited about the Solar Eclipse of 2017 and finding the perfect place to view it in the path of totality!
If you’re close to the path of totality, you’ll want to be there to have the full experience of seeing the sky go dark in the middle of the day. The path of totality is the only place where you can see the famous corona.
Grand Tetons, Wyoming
According to the American Astronomical Society, “It takes about 90 minutes for the Moon’s dark shadow to cross the country, starting around 10:15 am Pacific time on the West Coast and ending around 2:45 pm Eastern time (11:45 am Pacific time) on the East Coast. When you hear someone say, ‘the total eclipse lasts 90 minutes,’ that’s what they mean. But that could be misleading: At any given location within the path of the Moon’s shadow, the total eclipse lasts at most 2 minutes 40 seconds — don’t be late!”
This site shows the path of totality in each state that this path crosses. Twelve states will have at least part of the state within this path. Look at your state to see where you need to be to have the full eclipse experience.
On this site you can look at specific cities in your state to see which ones have the longest eclipse durations when the sky will be dark and the corona will be visible. Even though the darkness won’t last very long, you’ll have the eerie experience of night during the middle of day for the lengths of time at the locations listed in these charts.
Great Smoky Mountains, Tennessee
We at 36U enjoy traveling, and our travels have taken us to several places along the path of totality of this eclipse. The Grand Teton National Park in Wyoming, the Nine Mile Prairie in Lincoln, Nebraska, the University of Missouri in Columbia, Missouri, the Superman Statue in Metropolis, Illinois, the Great Smoky Mountains National Park in Tennessee, and the Cherohala Skyway in North Carolina all lie in the path of totality.
Look for a couple more 36U Solar Eclipse of 2017 blog posts before August 21st. We’ll be sharing some tips about eclipse viewing.
Total Solar Eclipse Part 1: Where Do I Go?
Total Solar Eclipse Part 2: What Do I Need?
Total Solar Eclipse Part 3: How to Plan
36U Blog Posts
Cherohala Skyway, North Carolina
Metropolis, Illinois
University of Missouri, Columbia, Missouri
Nine-Mile Prairie, Nebraska
THE Problem I Missed on the ACT Math Test
The original title of this post was supposed to be “The Math Problem I Had to Skip and Come Back To,” but it didn’t work out that way. I formulated the first title after I had to skip THE problem the first time.
I ended up missing the problem!
Recently, ACT Inc put out a new “Official ACT Prep Guide” and, as I always do, I sat down to take the tests (timed, of course) and to categorize the new items. This time, I set the timer and began working.
I was halfway through at the 19-minute mark and had no troubles. I noticed the problems were taking me a little more time than I wanted, but I only had a phone calculator and was only willing to use a small notepad to write something down if absolutely necessary.
No problems so far.
And then I hit #51:
(This item is owned by ACT Inc and printed in the first practice test in The Official ACT Practice Guide 2016-2017.)
I made a mental list of all possible perfect square sums from students 1 through 18: 4, 9, 16, 25. I started working and realized I couldn’t see the “quick way.”
Yes, almost all ACT Math items have a “quick way.” So, contrary to what I think most students should do at this point (which is to give it their best guess and move on), I skipped it.
I made my way through the rest of the test. The dumb “how many quarters are there?” problem. The Venn diagram problem. The Law of Sines. A probability distribution (That’s new!). And I headed back to #51…
I had about 4 minutes left at this point and decided to continue with the the brute force approach (another critical error?).
I eliminated choices A and C, because 1 + 16 and 1 + 9 don’t give perfect squares.
A little more deduction told me 17 had to be be paired with 8 to give the perfect square 25. Student 17 had to be paired with another student to give a perfect square. There wasn’t a student who could pair with 17 to reach the perfect square 36 (17 + 18 = 35). There was no way to pair student 17 with another student and get a number less than 17, so the only option was to add to 25. That made student 17 pair with student 8.
I was left with choices B and E.
I knew that 1 had to be paired with 3 or 15 (I had known that since the first pass through.). I scribbled. I paired. I scribbled. I paired.
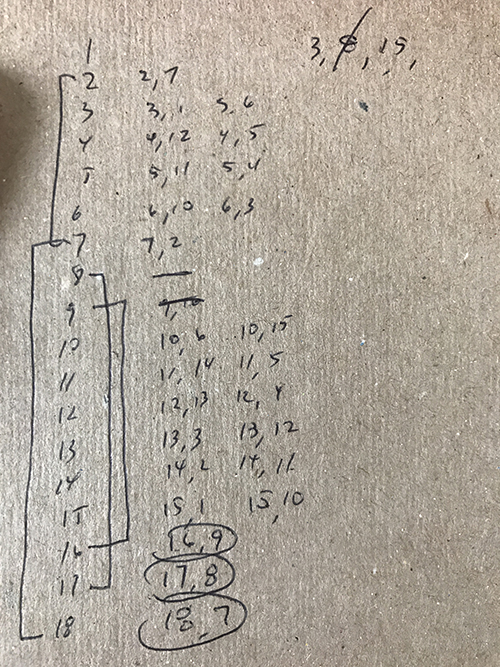
And I still didn’t get it. I was running out of time! I chose…3.
Wrong choice!
What Did I Do Wrong?
I’m not really sure where I went wrong. Is there a key that unlocks this problem quickly? I don’t know.
Eventually, I did figure that 1 had to be paired with 15, and this is how I did it…
Step 1: Start with the big numbers.
Pair student 18 with student 7, which is the only option for reaching a perfect square. Likewise, student 17 has to be paired with student 8. Student 16 has to be paired with student 9. Of the nine pairs, we have 3 pairs figured quickly!
Student 15 can be paired with student 10 (sum of 25) or student 1 (sum of 16).
Student 14 can be paired with student 11 (sum of 25) or student 2 (sum of 16).
Student 13 can be paired with student 12 (sum of 25) or student 3 (sum of 16).
Student 12 can be paired with student 13 (sum of 25) or student 4 (sum of 16).
Student 11 can be paired with student 14 (sum of 25) or student 5 (sum of 16).
Student 10 can be paired with student 15 (sum of 25) or student 6 (sum of 16).
Student 9 is already paired with student 16 (see above).
Student 8 is already paired with student 17 (see above).
Student 7 is already paired with student 18 (see above).
Student 6 can be paired with student 10 (sum of 16) or student 3 (sum of 9).
Student 5 can be paired with student 11 (sum of 16) or student 4 (sum of 9).
Student 4 can be paired with student 12 (sum of 16) or student 5 (sum of 9).
Student 3 can be paired with student 13 (sum of 16) or student 6 (sum of 9) or student 1 (sum of 4).
Student 2 can be paired with student 14 (sum of 16), not student 7 (already paired with student 18), not student 2, because he is student 2. We have our fourth pair! Student 2 is paired with student 14!
Student 1 can be paired with student 15 (sum of 16) not student 8 (already paired with student 17) or student 3 (sum of 4).
Step 2: Student 2 is the key.
Student 2 is paired with student 14. From there, work backwards from student to student eliminating possible choices until student 1’s pair is identified.
Go to the Student 14 line. Student 14 is paired with student 2, so that leaves student 11.
Student 11 can’t be paired with student 14. Student 11 is paired with student 5.
Student 5 is paired with student 11, so that leaves student 4.
Student 4 must be paired with student 12.
Student 12 is paired with 4. That leaves student 13.
Student 13 is paired with student 3. The leaves students 1 and 6.
Student 6 is paired with student 10, because student 3 is paired with student 3.
Student 10 is paired with student 6. That leaves student 15.
Student 15 must be paired with student 1!!!
Is there a better way?
For a 60 second per item pace, ACT is asking a lot in this problem.
Do you see a more efficient way to work this problem? If so, tell me how in the comments below.
Kendal Shipley, Ed.D.
8/29/2017
36U Blog Posts
ACT Reading Blog Post
Should I Skim the Questions Before I Read the Passage?
I get the “should I start with the questions?” question a lot. It’s a popular approach taught by many test prep helpers. The approach sounded like it had merit, so…
I sat down this week to do something I can’t remember ever trying before–skimming the questions before reading the passage and answering the questions on an ACT Reading test.
I thought skimming the questions would help me with the questions that were detail specific. I already knew there would be “big picture” questions dealing with theme and the purpose of paragraphs (because there are on every ACT Reading passage).
All items shown below are from the 2016-2017 Preparing-for-the-ACT Guide. They are the property of ACT Inc., not 36 University.
Here are the 10 questions I skimmed. I have highlighted the portions I initially underlined so you can see my thought processes and to help you read more quickly.
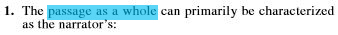
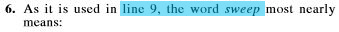
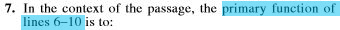
Here’s what happened:
- My initial skim seemed helpful. I knew I had to focus on photos by Bombay’s great photographers (Q1), several sets of lines (Q3, Q6, Q7, Q9), and how the narrator viewed his parents’ work (Q8), among others.
- But I had a hard time remembering the questions while trying to absorb the passage, and I knew absorbing the passage was essential because big picture items (Q1, Q7, Q8) were coming.
- I still had to reread the questions anyway. The questions were detailed enough so that I had to reread them to make sure there weren’t any nuances I missed in my initial skim.
- I ran out of time!!! It took me about 50 seconds to skim the questions. On average, you get 8 minutes and 45 seconds per passage. I went over that mark by about 15 seconds. That may not seem like much, but if I missed the pace by that much on all four passages, I’m a minute over the allowed time.
My Recommendation
I suggest reading the passage first. Keep a pace that allows you to remember key details while still soaking in the subtleties of the passage. Use the questions to guide you to parts of the passage that you may need to reexamine. They often specify paragraph or line placement to make your job even easier.
If you still think skimming the questions first is for you, I suggest you develop a quick notation system that helps you remember the questions and work through them more quickly when you get back to them. Practice enough so that you know which types of questions you want to try to keep in mind as you read the passage. Ultimately, check your approach (using a practice test) versus the more traditional passage-then-questions approach to see which one gives you the best score.
Dr. Kendal Shipley, 36U President
5/25/2017
The Six Trickiest Math Problems We Found on the Most Recent ACT
If you learned what your teachers taught in your math classes, then you should do great on the ACT math test. However, like most standardized tests, the ACT will throw a few items your way that look a little different than the items your teacher assigned.
So, here are the tricky items we found on the latest publicly-released ACT. There are six of them. Have questions or comments? Let us know! Please note: these aren’t necessarily the most difficult items on the math test, though some are, but they are the ones that we consider the slyest.
All items shown below are from the 2016-2017 Preparing-for-the-ACT Guide. They are the property of ACT Inc., not 36 University.
Tricky ACT Math Item #6
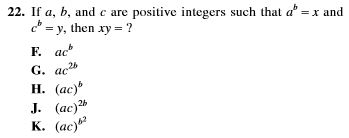
What’s Tricky About It?
This item is asking for an application of an exponents rule, but in a way that isn’t usually stressed in math classrooms. Usually, students are taught to distribute exponents to the bases:
(ab)x –> axbx
But this problem asks students to apply the same concept, but in reverse.
How You Should Work It
The problem asks for x•y.
Step 1) Use the information from the problem (x = ab and y =cb) to substitute for x and y.
x•y –> abcb
Step 2) Apply the exponent rule (ab)x –> axbx in reverse. In other words, both bases have the same exponent, so the exponent can be placed outside parentheses:
abcb –> (ac)b
The answer is H.
Tricky ACT Math Item #5
What’s Tricky About It?
Monthly payment. P dollars. Short-term loan. Annual interest rate. This item is wordy, and the vocabulary is a little tough. On top of that, that equation is intimidating.
On top of that, many students won’t know how to handle multiplying a by 2.
How You Should Work It
Step 1) Multiply a by 2.
Here’s the new value for p:
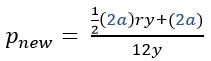
Step 2) Factor out the 2.
Don’t make this too complicated: use the distributive property in reverse.
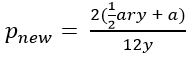
and because multiplying the numerator by 2 is the same as multiplying the fraction by 2:
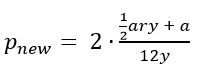
Step 3) Compare to the previous value for p.
In the problem, the value for p was:
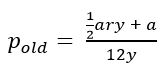
When a is multiplied by 2, p is also multiplied by 2. The answer is D.
Tricky ACT Math Item #4
What’s Tricky About It?
Reasoning through this item, especially with its fractions, is very difficult. Only the top students may find that a navigable path.
How You Should Work It
The easiest way to work the item is to set up an equation that mirrors the situation.
Let x = volume of the container in cups
Step 1) Set up the equation.
The problem says they took 1/8 of the container, added 10 cups, and ended with the container 3/4 full. Or, maybe this is simpler: One-eighth of the container plus 10 cups equals three-fourths of the container.
As an equation, that description looks like this:
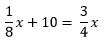
Step 2) Solve the equation for x, the volume of the container.
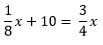
Subtract (1/8)*x from both sides.
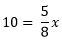
Multiply both sides of the equation by 8/5.
x = 16 cups
The answer is J.
It’s also a good practice to check your solution with the information given in the problem. Have fun!
Tricky ACT Math Item #3
What’s Tricky About It?
Students are often more comfortable working from point A to point B along a path they’ve trod several times before. This item invites students to reason to try to find the relationship between x and z, but that reasoning is difficult.
How You Should Work It
There is a variable common in both ratios—y. Rewrite both ratios so that y has the same value in both.
Step 1) Rewrite both ratios.
The variable y corresponds with the 2 in the first ratio and a 3 in the second ratio. Rewrite both ratios so that y has a value of 6 (least common multiple).
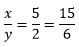
and
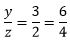
Step 2) Make the comparison between x and z.
Rewriting both ratios as fractions with a y value of 6 allows us to compare x and z.
If the ratio of x to y is 15 to 6 and the ratio of y to z is 6 to 4, then the ratio of x to z is 15 to 4.
The answer is E.
Tricky ACT Math Item #2
What’s Tricky About It?
This item, like a few others in this list, is likely to have students spending an inordinate amount of time with a trial-and-error method trying reason their way to the answer. That is a tough road!
How You Should Work It
Students need a Venn Diagram in their math tool chest. Unfortunately, many of them may not have used a Venn Diagram since the 8th grade.
Set up a Venn Diagram for all 120 students.
Step 1) Survey question one tells us that 55 students have neither skied cross-country or downhill.
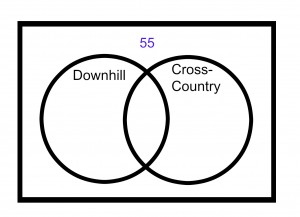
Step 2) Use survey questions two and three to find the number of students who have skied both cross-country and downhill.
Survey question one states that 65 students have either skied cross-country or downhill. Survey question two states that 28 have skied downhill and 45 have skied cross-country. That’s 73 total, 8 more than the 65 from Q1. That means some of them have done both!
Take the surplus of 8 and place them in the overlap for students who have skied both downhill and country-country.
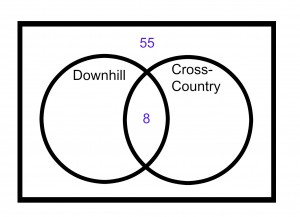
Step 3) Use survey questions 2 and 3 to finish out the Venn Diagram.
Twenty-eight students have skied downhill.
Forty-five students have skied cross-country.
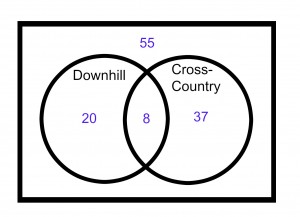
Step 4) Check your Venn Diagram with the original information.
After your check, you’ll see that indeed 8 of the students had skied both cross-country and downhill.
The answer is E.
Tricky ACT Math Item #1
What’s Tricky About It?
There are two difficulties here:
1) Rate problems are standard fare in algebra class, but this item isn’t worked like most of those textbook problems are worked.
2) The wording is strange. Who ever asks about how many cans of food a dog eats in “’3 + d days?’”
How You Should Work It
Step 1) Recognize the rate at which the dog is eating.
Seven cans in three days means the dog is eating 7/3 of a can per day. This means that you can take the rate (7/3 of can per day) and multiply by the number of days to get the total amount of dog food consumed.
Try this: After 3 days the dog has eaten (7/3) * 3 = 7 cans of food, just like the problem stated.
Step 2) Substitute to find the solution.
How many cans does the dog eat in 3 + d days? Break this into two separate parts. In 3 days, the dog eats 7 cans, just like the problem told us. In d days, the dog eats (7/3)*d cans, just like we figured in Step 1. This means the dog eats 7 + (7/3)*d cans.
The answer is K.
Solution Page
The Locker Problem
We want thank all who attempted the January 2017 Math Challenge. We hope you enjoyed and learned from the problem.
For those who missed it, here was the challenge problem:
Imagine 100 lockers numbered 1 to 100 with 100 students lined up in front of those 100 lockers:
The first student opens every locker.
The second student closes every 2nd locker.
The 3rd student changes every 3rd locker; if it’s closed, she opens it; if it’s open, she closes it.
The 4th student changes every fourth locker.
The 5th student changes every 5th locker.
That same pattern continues for all 100 students.
Here’s the question: “Which lockers are left open after all 100 students have walked the row of lockers?”
The Solution
As many of you found, the perfect square lockers (#s 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100) are the only lockers left open. Cool, huh?
We hope you realized that lockers are only touched by students who are factors of that locker number, i.e. locker #5 is only touched by students 1 and 5. Student 1 opens it and student 5 closes it. In fact, because factors come in pairs, the first student factor will open it and the corresponding factor student closes it. At first, maybe you thought every locker would be closed because factors come in pairs. But there was a twist…
Here are a couple of ways you could have gotten there:
Method 1: Solve a Simpler Problem
Start with just 20 lockers and try to find a pattern.
We used a code: O = Open, C = Closed.
Here’s what the lockers look like after the first student walks through. They are all open.
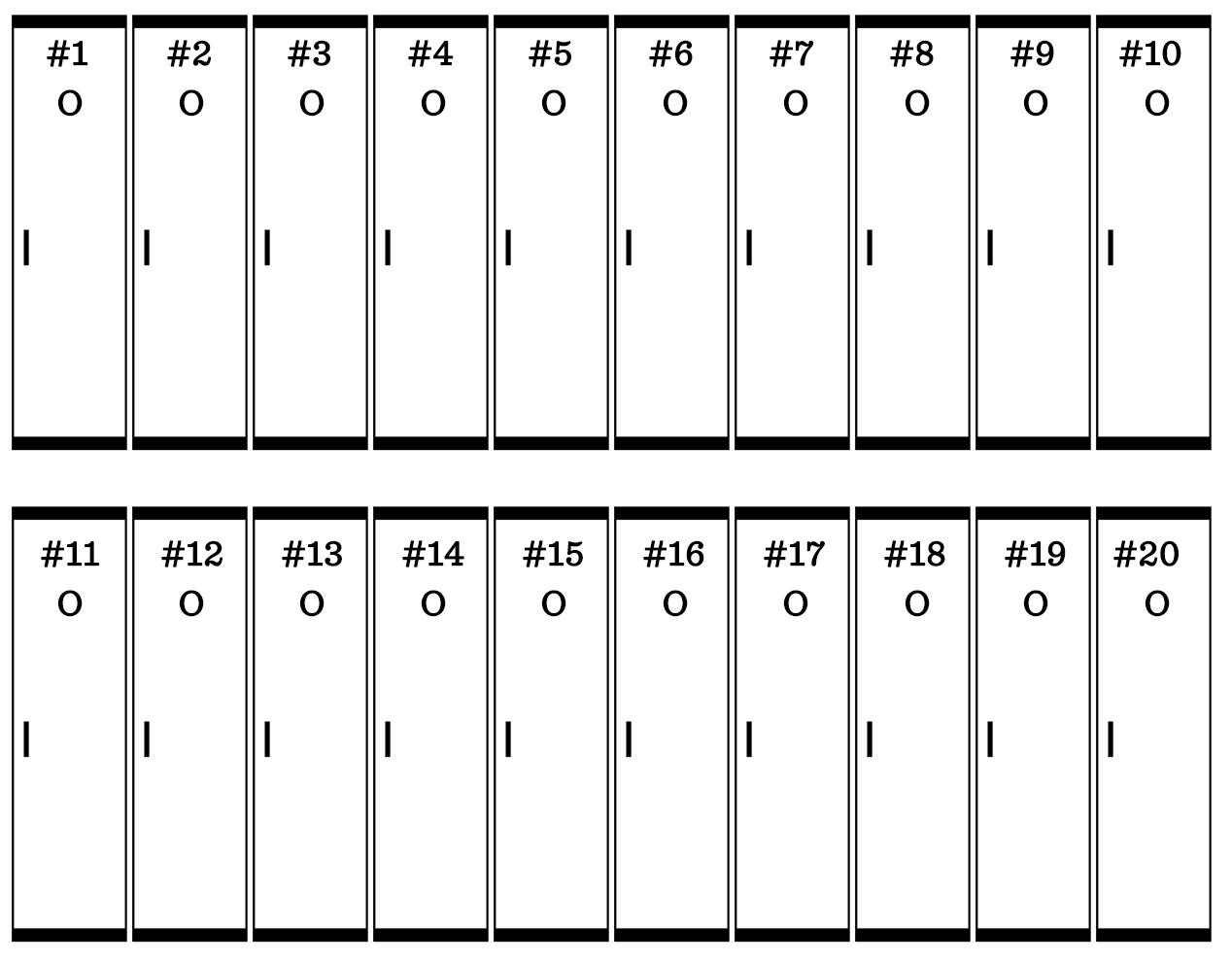
After the second student walks the row of lockers, the odd-numbered lockers are left open and the even-numbered lockers are closed:
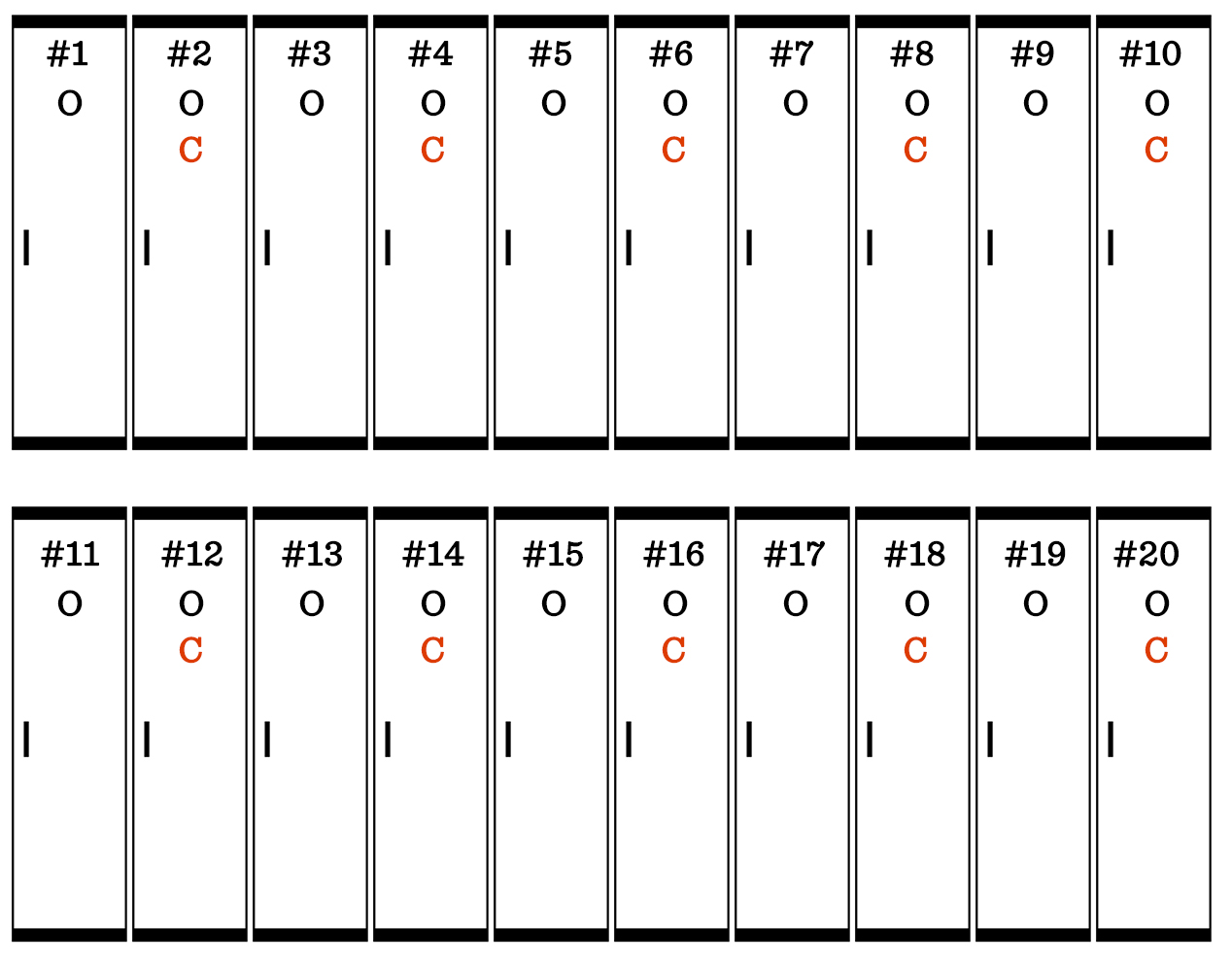
Here’s how the lockers look after the third student changes every 3rd locker:
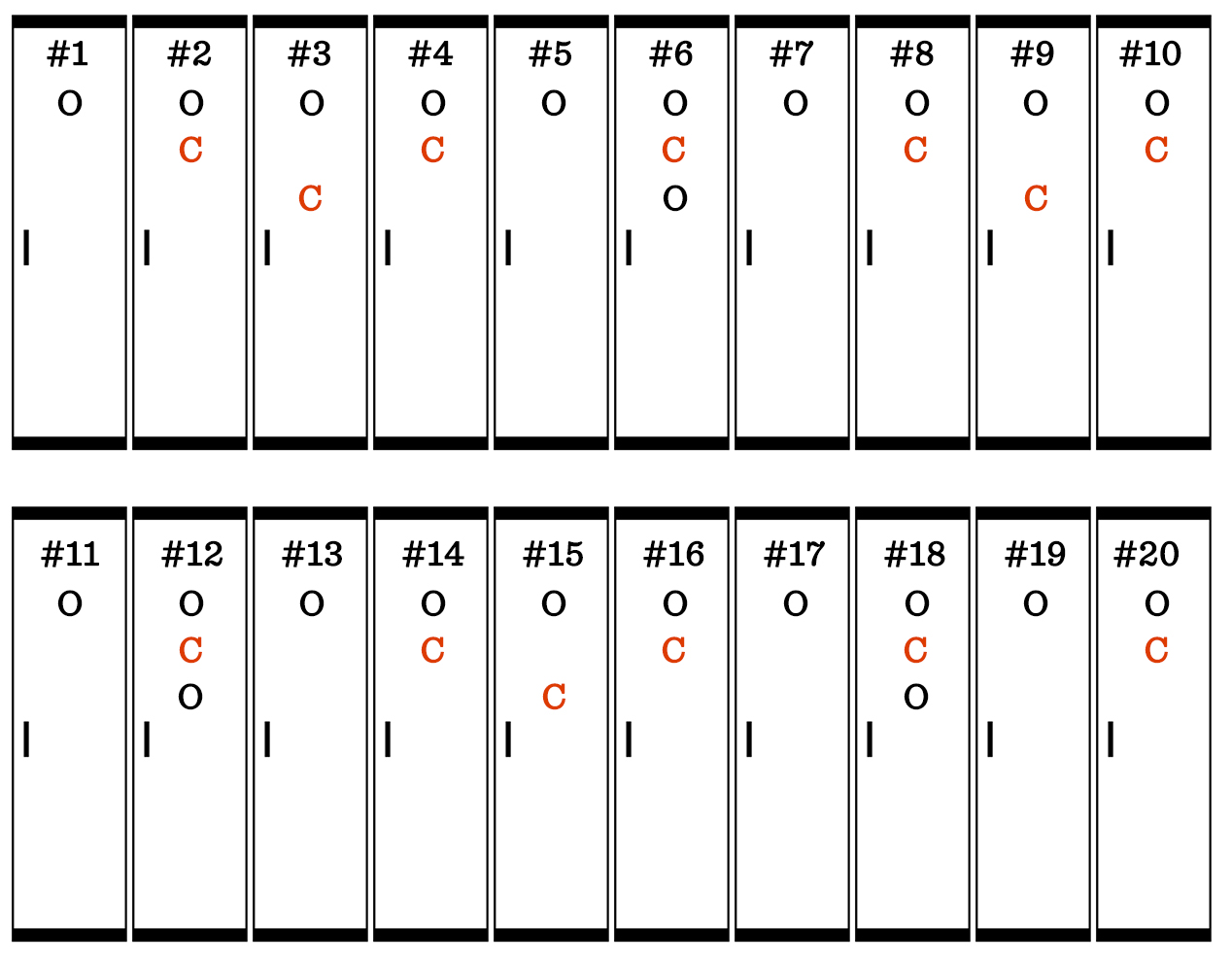
And here’s how it looks after the first 20 students have walked the row of lockers. Note: after student 20 has gone, the first 20 lockers aren’t touched again.
Of the first 20 lockers, locker #s 1, 4, 9, and 16 are left open. Those are perfect squares. You can extend that pattern to identify the remaining open lockers.
Lockers 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are left open!
Method 2: Who Touches Which Lockers
Identifying which students touch which lockers is a little less of a brute-force approach and would likely have gotten you to the solution a little more quickly.
Here’s what I mean:
Consider locker #1. The only student who touches locker #1 is student #1. Student 1 opens the locker, and since no one else touches it, it will be left open at the end.
Consider locker #2. Student 1 opens the locker, and student 2 closes it. No one else touches the locker, so it will be closed.
Consider locker #10. Students 1 opens the locker. Student 2 closes it. Students 3 and 4 skip right by it. Student 5 opens it. Students 6, 7, 8, and 9 skip right by it. And student 10 closes it. Locker #10 will be closed.
Mental Milestone 1: After looking at several lockers, you should notice that lockers are only changed by student numbers that are factors of the locker number. In other words, locker 12 is changed by students 1, 2, 3, 4, 6, and 12.
Mental Milestone 2: You should also have noticed that factors always come in pairs. This means that for every student who opens a locker, there is another student who closes it. For locker #12, student 1 opens it, but student 12 closes it later. Student 2 opens it, but student 6 closes it later. Student 3 opens it, but student 4 closes it later.
By this logic, every locker would be closed.
But there are exceptions!
Consider locker #25. Student 1 opens it. Student 5 closes it. Student 25 opens it. The locker will be left open, but why? In this case, the factors do not come in pairs. One and 25 are a pair, but five times five is also 25. Five only counts as one factor. This causes the open-close pattern to be thrown off. Locker #25 is left open.
Mental Milestone 3: When factors don’t come in pairs, the locker will be left open. And factors don’t come in pairs when numbers are multiplied by themselves. Perfect squares (1, 4, 9, 16, 25, 36, 49, 64, 81, 100,…) are the only numbers whose factors don’t come in pairs because one set of factors, the square root, is multiplied by itself. This means that only perfect square lockers will be left open.
Locker #s 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are left open!
The Winner
Congratulations to Sydney H, our January 2017 ACT Challenge winner! Her solution was simple, precise, and just as important, correct. In fact, I like her solution better than the explanations I provided above. Here’s what she had to say:
The Winnings!
Sydney won the 36U Winter Care Package:
3 months access to 36U ACT Prep
36U Tee (Long-sleeve)
36U toboggan
$15 Starbucks gift card
More 36U Resources:
36U Blog Posts
36U ACT Tips
36U ACT Prep Program
The Locker Problem – January 2017 Challenge
Number properties are rarely reviewed, but they are sometimes tested on the ACT. So, we’ve decided to share a fun, straightforward, and hopefully enlightening item that will have you thinking about number properties. Here’s your January 2017 ACT Math Challenge:
Imagine 100 lockers numbered 1 to 100 with 100 students lined up in front of those 100 lockers:
The first student opens every locker.
The second student closes every 2nd locker.
The 3rd student changes every 3rd locker; if it’s closed, she opens it; if it’s open, she closes it.
The 4th student changes every fourth locker.
The 5th student changes every 5th locker.
That same pattern continues for all 100 students.
Here’s the question: “Which lockers are left open after all 100 students have walked the row of lockers?”
How Do I Enter?
Take a pic of your solution, with your work included, and post as a reply to any of our Locker Problem social media posts or send to lockerchallenge@36university.com. Submissions must be posted by midnight eastern time on January 31st. Impress us with your approach to solving this problem!
What Will I Win?
The winner will receive the 36U Winter Care Package:
3 months access to 36U ACT Prep
36U Tee (Long-sleeve)
36U toboggan
$15 Starbucks gift card
How Will 36U Choose a Winner?
At 36U, we value simple, precise solutions. We will draw a winner on February 1st from among entries with correct answers and easy-to-understand explanations. (or: whose solutions are correct and whose approach is easily understood.)
More 36U Resources:
36U Blog Posts
36U ACT Tips
36U ACT Prep Program
ACT English: Should I Choose Who or Whom?
If you’re like many students, you may find the ACT questions dealing with who/whom a bit daunting. Recently one of my ACT Crash Course students stayed after class to ask, “How do I know whether I should choose who or whom? I get confused!”
My quick answer was that whom is used as the object of a preposition. I gave him examples, “To whom, for whom.”
After giving his question a little more thought, I decided a more in-depth response is in order. I reviewed all of the occurrences of who/whom items on recently released ACTs, and here’s what I think students need to know…
Who as the Subject
Who is a pronoun that works as a subject. This means that the word who can take the place of the subject, and it will be doing the action!
English Pro Tip #1: Choose who when the pronoun is used as a subject (doing the action).
Sentences that just rename the subject make choosing who easy:
Who is doing the action – spotting the grizzly bear – so who is the right form.
Whom as the Object
Whom is the object form of the pronoun who. If the pronoun is having the action done to it as the target of the action, the pronoun is serving as an object pronoun — in that case, choose whom!
English Pro Tip #2: Choose whom when the pronoun is the object or target (the action is being done to it).
I invited my friend to travel with me. Whom is the target of the action, so it’s the right choice here.
Whom as the Object of a Prepositional Phrase
Recognizing a prepositional phrase and choosing whom as the object makes for the easiest of your who-or-whom choices.
English Pro Tip #3: Use whom when the pronoun is used as the object of a preposition.
However, just because who follows a preposition, that does not mean it is serving as the object of the preposition. Take a look at this sentence:
She kept you from getting information about who is planning the party.
Who is serving as a subject pronoun doing an action – planning the party. In this sentence, who is the correct choice.
————————Quick Check: How Will This Look on the ACT?————————
1. The students that toured Mammoth Hot Springs also swam in Yellowstone’s Boiling River later in the evening.
A. NO CHANGE
B. that swam in Yellowstone’s Boiling River later that evening also toured Mammoth Hot Springs.
C. who toured Mammoth Hot Springs relaxed by swimming in Yellowstone’s Boiling River later that evening.
D. are swimming in Yellowstone’s Boiling River, after which they toured Mammoth Hot Springs.
2. The Old Faithful Inn recruits high school students who travel from all over the country to work during the summer.
A. NO CHANGE
B. students of which
C. students, those who
D. students, of whom
3. The park ranger found the students to whom the bison had charged.
A. NO CHANGE
B. those who
C. whom
D. that which
4. Yellowstone National Park attracts thousands of visitors each year, many of them come to see Old Faithful.
NO CHANGE
of whom
of who
DELETE the underlined portion.
Answers:
1. C — Choice C uses the pronoun who to refer to the students instead of the pronoun that (choices A and B). The pronoun is also doing the action — touring — so who is the correct form.
2. A — The pronoun who is used as a subject pronoun and is doing the action (traveling).
3. C — The bison charged the group of students. The object form of the pronoun — whom— is the right choice. Choice A is wrong because the wording is awkward. Choose C.
4. B — The pronoun is the object of the preposition. Choose of whom. Choices A and D both create comma splices (two complete thoughts connected with a comma).
More 36U Resources:
36U Blog Posts
36U ACT Tips
36U ACT Prep Program
